Quaternary Structure

Although a substantial number of proteins function as monomers there are many others that exist as multimers. The arrangement of protein subunits in a macromolecular assembly is referred to as its quaternary structure. This aspect of protein structure plays an important role in the stability and regulation of a large number of enzymes, virus assembly, cellular regulation, and motility. Indeed, quaternary structure underlies all aspects of protein–protein interaction.

The magnitude of protein–protein interfaces varies enormously from ∼800 Ų to over 4000 Ų per subunit. There is considerable variation in the nature of the interface. Some interfaces are very similar to the hydrophobic core the protein, whereas others contain a substantial polar component and solvent pockets. Thus the stability of a multimeric assembly is only loosely proportional to the surface area buried on formation of the multimeric assembly. As might be expected from considerations of protein stability, the overall stability of multimeric assemblies is proportional tothehydrophobicsurfaceareaburied within the interface.

A large number of enzymes exist as symmetric macromolecular assemblies where they commonly exhibit C and D point group symmetries and contain two-, three-, four-, and six-fold axes of symmetry. In the simplest cases this feature provides additional thermodynamic stability for a protein that would otherwise be rather small. In more complex arrangements the protein–protein interfaces form the active site such that the oligomerization is required for function. Finally, in the most highly evolved enzymes there is communication between the active sites that reside on symmetrically related subunits. This provides the foundation for enzyme regulation as observed in most allosteric enzymes.

A. Allosteric Enzymes
The simplest model for allosteric control was set forward by Monod, Changeux, and Jacob in 1963 and provided the basis for understanding feedback inhibition and cooperative binding of ligands by proteins. In their model it was assumed that an allosteric enzyme (or protein) exists in equilibrium between two symmetric states; inactive and active (T and R states). The transition between these states was assumed to be concerted, that is the symmetry of the macromolecular assembly is conserved. Furthermore the active state has a greater affinity for substrate than the inactive state. From these considerations the activity of the enzyme depends on the position of the equilibrium between the inactive and active states. Thus increasing the substrate concentration drives the equilibrium to the active form and gives rise to a sigmoidal relationship between the initial velocity of the reaction and the substrate concentration. As importantly the position of the equilibrium can be altered by allosteric effectors that preferentially bind to either the inactive or active state. This is the basis of feedback inhibition whereby the product of a biosynthetic pathway inhibits the enzyme that catalyzes the first committed step. This simple model explains many of the properties of allosteric enzymes; however, a more complex model based on sequential binding of substrates to yield multiple conformation states is required to explain the finer details of many enzymes.

The structural basis of allostery has been well developed through the study of enzymes such as aspartate transcarbamoylase and phosphofructokinase. In all enzymes studied thus far several common themes have evolved. First the overall symmetry of the inactive and active states appear to be conserved. Second the transition between these states involves a change in the relationship between the protein subunits that serve to alter the position of the polypeptide chains or cofactors within the regions responsible for ligand binding or catalytic activity. Allosteric effectors serve to either inhibit or enhance these conformational changes. Thus in all cases the active site residues are influenced either directly or indirectly by the protein– protein interactions between subunits. Typically a rotation of subunits of 5–15° is sufficient to accomplish allosteric control.

B. Viruses

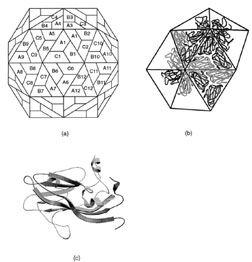FIGURE 18 Structural arrangement of capsid proteins in southern bean mosaic virus. (a) The surface lattice describing the relationship between the three groups of 60 identical subunits. (b) The arrangement of protein subunits on the surface of the virus. (c) A ribbon representation of viral coat protein for position A.

Viruses represent particularly evolved forms of macromolecular assemblies. Mature virions are encoded by a protective coat that is formed in part by virally encoded proteins. Viruses come in many shapes and sizes, but they all share the property of using multiple copies of coat proteins to protect their genomic material. In many cases the proteins assemble to form a symmetric shell, where the symmetries are either helical as found in tobacco mosaic virus or icosahedral as seen in the spherical viruses. The use of multiple copies of a protein to form a viral coat is enormously efficient from a genomic point of view; however, it introduces several interesting structural problems.

All simplespherical viruses exhibit icosahedral symmetry. This implies that the surface contains 60 equivalent positions or that the shell is built from 60 equivalent protein subunits. Although this is observed for a few very small virus particles, most contain many more than 60 subunits. For example the viral shell of most small plant viruses contains 180 identical protein subunits. This poses a problem of how to arrange 180 subunits on the surface of an icosahedral shell since the subunits cannot experience symmetrically equivalent environments. Fifty years ago it was proposed by Caspar and Klug that viral subunits would be arranged on a hexagonal surface lattice with quasiequivalent symmetry where the contacts between subunits would be organized to minimize their differences in assembly. That is, if a virus contains 180 subunits on its surface, these would be grouped into three sets of 60 subunits where each group would experience similar interactions compared to the other groups. At first sight this hypothesis accounts for the structure of simple viruses where it has been shown that most of the interactions between the protomers on the surface are essentially identical; however, closer examination of the virus structures that have been determined reveals that in all cases the groups of protomers behave as though they are different proteins by utilizing their domains in different ways to accommodate their structurally unique environments (Fig. 18). Thus, it would appear that the main requirement for a virus coat protein is to have a shape and conformational flexibility to allow them to form a cohesive shell, without compromising the structural integrity of the quaternary interactions. These latter principles may be applied to all viral coat proteins.