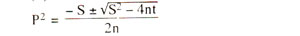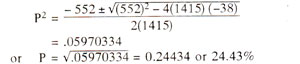Test cross data like the above obtained in a three point test-cross are not always available and can not be easily obtained. In such cases, if two linked genes exhibit complete dominance, recombination frequencies can be calculated from F
2 data. These data can be obtained easily and routinely from F
1 x F
1 crosses or by selfing F
1 individuals (in plants). As a first step, the data will be subjected to
chi-square (χ
2) test for independence (see later in this section). If the test indicates significant deviation from expected results, recombination frequencies can be calculated.
If we assume a recombination frequency of P between two genes
A and
B, then in gametes derived from
AaBb, the frequencies of recombinant gametes will be P/2 each and the parental types will be (1 - P)/2 each. From these gametic frequencies, expected zygcjtic frequencies can be calculated using a checkerboard. The summarized results from such calculations are given in Table 10.3. Utilizing information given in this table, one of the following two methods can be used for calculating recombination frequencies from F
2 data.
Product ratio method. The F
2 data is derived from a heterozygote such
as AaBb, which in its turn may be derived from parents either in coupling phase
(AABB x
aabb) or in repulsion phase
(AAbb x
aaBB). In both cases, if independent assortment holds good, then
9AB : 3Ab : 3aB : lab ratio should hold good. If chi-square test gives lack of independence between
A and
B, recombination frequencies can be calculated from the product ratio (z) derived as follows, where
AB = a,
Ab = b,
aB = c and
ab = d
(1) Coupling phase (AABB x
aabb→
AB/ab→
F2) z = (b x c)/(a x d)
(2) Repulsion phase (AAbb x
aaBB→
Ab/aB→
F2) z = (a x d)/(b x c)
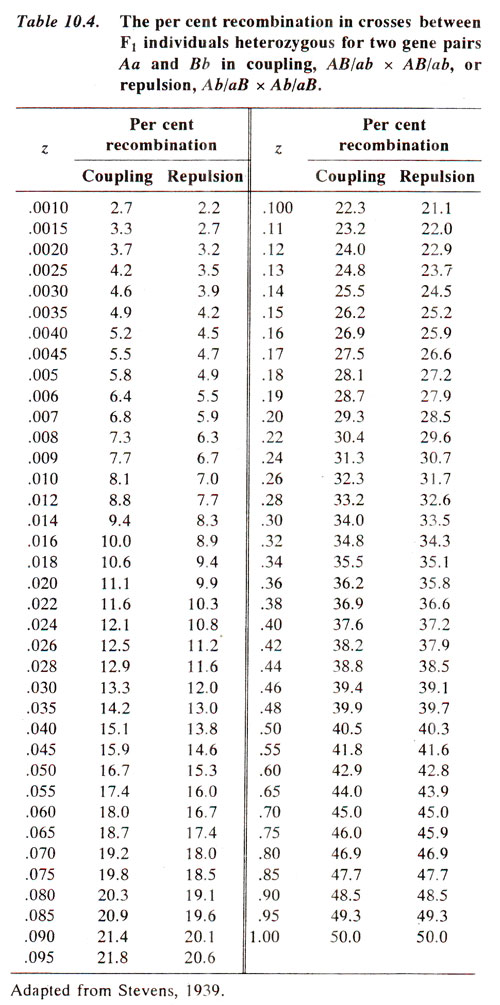
The recombination frequency P (as per cent) can be obtained for calculated value of
z from the Table 10.4.
Maximum likelihood method. This method is based on the principle that a recombination value (P), whose variance is minimum, will be the best estimate of recombination frequency. Therefore, P value is calculated using differential calculus, so that the probability of getting the observed results is maximum. Without giving the mathematics involved in the derivation of the formula used for such computation, we like to give here the final formula used for computation of recombination value (P).
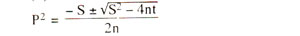
where, S = - (a - 2b - 2c - d)
t = - 2d
n = (a + b + c + d)
As an illustration, suppose in a cross, following F
2 data (n = 1415) are obtained : a = 753, b = 292,
c = 351 and d = 19. The values can be substituted in the above formula as follows :
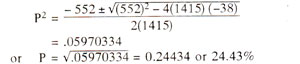
Prediction of F2 ratios for linked genes. If
recombination frequency (P) is given, for linked genes one can also calculate the relative frequencies of different genotypes and phenotypes expected in F
2 generation. For instance, if P = 10%, then the gametic frequencies will be :
AB = .45,
ab = .45,
Ab = .05,
aB = .05. From this information, using a checkerboard, frequencies of 16 possible combinations can be calculated, e.g.
aabb = .45 x .45 = .2025 = 20.25%. In terms of recombination frequency, P, the proportion of
AB/AB or
ab/ab can be expressed each as
¼ (1 - P)
2 in coupling phase, and as
¼P
2 in repulsion phase.