The rules of probability (product rule and sum rule)

When the number of genes increases beyond three, the number of possible phenotypes and genotypes increases exponentially, so that even the forked line method may become unwieldy. In such cases, we may have to use the rules of probability, which are briefly described in this section.


Definition of probability
Probability of an event is the likelihood of its occurrence. This probability in some cases is available 'a priori', but in other cases it may have to be calculated through an experiment. For instance, on tossing a coin, probability that it will fall head i.e. p(H) = 0.5. Similarly on rolling a six sided dice, the probability of getting a six i.e. p(6) = 1/6. In genetics, on selfing a heterozygote (Aa), probability of getting 'aa' i.e. p(aa) = 1/4. In other cases, for instance, the probability of getting high yield from a crop in a particular year will be obtained through calculations from the available data.

The product rule (or multiplication law)
This rule states that the probability of simultaneous occurrence of two or more independent events is the product of the probabilities of occurrence of each of these events individually. Therefore, if the probabilities of the occurrence of gametes with I and i in heterozygote Ii and those of R and r in a heterozygote Rr are, p(I) = ½, p(i) = ½, p(R) = ½, p(r) = ½, then the probabilities of gametes with IR, Ir, iR, ir in a heterozygote IiRr can be calculated on the basis of the product rule in the following manner

p(IR) = p(I) x p(R) = ½ x ½ = 1/4

p(Ir) = p(I) x p(r) = ½ x ½ = 1/4

p(iR) = p(i) x p(R) = ½ x ½ = 1/4

p(ir) = p(i) x p(r) = ½ x ½ = 1/4

Thus in a heterozygote IiRr, the probabilities or IR, Ir, iR and ir are 1/4 each, as shown above. Similarly the probabilities of the occurrence of each double homozygote like IIRR or IIrr or iiRR or iirr can be calculated as 1/4 x1/4 = 1/6. For calculating probabilities of different phenotypes, the product rule has also been used in Table 2,3. However, for calculating probabilities of heterozygotes like IiRr, first consider that it may result from any of the following four events, IR (♀) x ir (♂) or Ir (♀) x iR (♂) or iR (♀) x Ir (♂) or ir (♀) x IR (♂). The probability of each of these events will be calculated from the product rule but that of all of them including any one of them leading to same genotype will be calculated following the sum rule or addition law (given below).

Using a more complex example of five genes, the probability of getting AAbbCcDdeeFf from a cross AaBbCcDdEeFf x AaBbCcDdEeFf can be calculated as follows : p(AAbbCcDdeeFf)

= p(AA) x p(bb) x p(Cc )x p(Dd) x p(ee) x p(Ff)

= ¼ x ¼ x ½ x ½ x ¼ x ½

= 1/512

The sum rule (or addition law)
This rule states that the probability of the occurrence of either one or the other of two or more mutually exclusive events is the sum of their individual probabilities. For instance, if there are more than one genotypes, each of them giving the same phenotype, then this is an Either/Or situation and the probabilities of each such genotype will be summed to get the probability of the phenotype. For instance if probability of IIrr and Iirr are 1/16 and 2/16respectively, the p(yellow and wrinkled) = 1/16 + 2/16 = 3/l6. Similarly, in F₂ the probability of getting a phenotype dominant for both traits I and R will be : p(IR phenotype)

= p(IIRR) + p(IIRr) + p(IiRR) + p(IiRr)

= 1/16+ 2/16 + 2/16 + 4/16

= 9/16

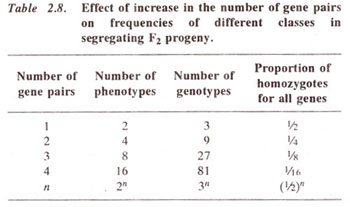
The number of genotypes and phenotypes, whose probabilities can be calculated on the basis of the rules of probability, are shown in Table 2.8 for different numbers of segregating pairs of genes.