How Algae Move
Cytoplasm, cell walls, and skeletons of algae have a density greater than the medium these organisms
dwell in. The density of fresh water is 1.0 g cm
-3 and that of sea water ranges from 1.021 to 1.028 g cm
-3, but most cytoplasmic components have a density between 1.03 and 1.10 g cm
-3, the silica forming the diatom frustule and the scales of Chrysophyceae have a density of 2.6 g cm
-3, and both calcite and aragonite of Haptophyta coccoliths reach an even higher value of 2.7 g cm
-3. With this density values, algae must inevitably sink. Therefore, one of the problems facing planktonic organisms (organisms that wander in the water or are carried about by the movements of the water rather than by their own ability to swim) is how to keep afloat in a suitable attitude between whatever levels are suitable for their life. The phytoplankton must obviously remain floating quite close to the surface because only here is there a sufficient illumination for photosynthesis.
There are broadly two solutions by which algae can keep afloat and regulate their orientation
and depth: a dynamic solution, obtaining lift by swimming; and a static solution, by buoyancy
control, or through adaptations reducing sinking rates. In many cases the two solutions function
together.
Swimming
What does it mean to swim? It means that an organism immersed in a liquid environment is allowed
to deform its body in the same manner. The algae are all good movers or better good swimmers.
They swim more or less continuously and control their level chiefly by this means. For example
dinoflagellates, which can achieve speeds of 200–500 µm sec
-1, are said to maintain themselves near the surface by repeated bursts of upward swimming, alternating with short intervals of rest during which they slowly sink. Motility is present in unicellular algae or colonies that are propelled by flagella; in some classes it is confined only to gametes and asexual zoospores provided with flagella, which are used as motor system for their displacement in the fluid medium.
In order to move through a fluid the swimming cell must use its motor system to push a portion
of the fluid medium in the direction opposite to that in which the movement is to take place.
Forward movement of a swimming alga is resisted by two things: the inertial resistance of the
fluid that must be displaced, which depends on the density of the fluid and the viscous drag experienced by the moving organism, that is, the rearward force exerted on the organism by the fluid molecules adhering to its surface when it passes through the viscous fluid. The ratio of inertial and
viscous forces is the Reynolds number (R), which depends on the size of the organism (related
to the linear dimension, (
l)), its velocity (
u), and to the density (
ρ) and viscosity (
η) of the fluid medium according to the equation:
As the ratio between the viscosity and the density is the kinematic viscosity (
ν in cm
2 sec
-1), Equation (2.1) can be written as:
In water the kinematic viscosity is 10
-2 cm
2 sec
-1.
An algae 50 µm long swimming at 10 µm sec
-1 has the minuscule Reynold’s number of 5 x 10
-4, hence inertial effects are vanishing and the major constraint is the viscous drag; this means that what an algae is doing at the moment is entirely determined by the forces that are exerted on it
at that moment and by nothing in the past. Therefore, when the flagellum stops, forward movement of the cell will cease abruptly without gradual deceleration.
Reynolds number might get up to 10
5 for a fish long 10 cm swimming at 1 m sec
-1. If the same fish would be swimming at the same Reynolds number of an alga, it would be as if it was swimming inside molasses.
Another funny thing about motion at low Reynolds number is reciprocal motion. As time does not matter the deformation that produces the swimming must be asymmetrical. Therefore, the pattern of flagellar beating must be three-dimensional and asymmetric, that is, the forward stroke should be different from the reverse.
For optimum propulsive efficiency, cell body size should be 15–40 times the flagellum radius
(about 0.1 µm), and this ratio is present in many algae. When the cell body size is larger than predicted, as in Euglena, the effective radius of the flagellum is modified by simple, non-tubular hairs.

FIGURE 2.58 Negative staining of the trailing flagellum of Ochromonas danica. (Bar: 1 µm.)
Beat patterns of most smooth flagella (i.e., without hairs) are three-dimensional, and the analysis
of the motion is far from straightforward. However, it is clear that the direction in which the
microorganism moves is opposite to the direction in which the waves are propagated along the
length of the flagellum, so that in almost all cases, when the cell body is to be pushed along, a
wave must be initiated at the base of the smooth flagellum. Although basal initiation is more
common than distal, both are known. The velocity of forward movement is always a small fraction
of the velocity of the wave running along the flagellum, and its propulsive efficiency depends on the
ratio of its amplitude and wavelength. Unlike smooth flagella, the propulsive force generated by a
flagellum bearing tubular hairs is in the same direction as the direction of wave propagation. These
stiff hairs remain perpendicular to the axis of the flagellum as it bends (Figure 2.58). A wave
moving away from the cell body will cause the hairs to act as oars and the overall effect will be
to propel the cell flagellum first.

FIGURE 2.58 Negative staining of the trailing flagellum of Ochromonas danica. (Bar: 1 µm.)
Control characteristics, and thus behavioral peculiarities, are connected with the functioning of
the propelling structure of the cell. If the cell is asymmetric, it advances spinning along its axis; it can correct its trajectory only by sudden steering obtained by changing the insertion angle of flagella, or by the stiffening of internal structures. This behavior can be attributed to all heterokont or uniflagellate algae. In the case of a symmetric cell, it can accomplish a gradual smooth correction of its trajectory going forward without spinning (or rotating with a very long period), and displacing the barycenter of the motor couple. This behavior can be attributed to all isokont cells.
Examples of main swimming patterns among algae will be described as follows.

FIGURE 2.59 Swimming pattern of Ochromonas danica.
In
Ochromonas sp. (Heterokontophyta) only the flagellum bearing hairs seems to be active
during swimming. It is directed forward and executes simultaneous undulatory and helical waves that travel from its base to the tip. The resulting flagellum movements cause the whole body of the cell to rotate as it moves forwards. The shorter flagellum trails backward passively, lying against the cell; it is capable of acting as a rudder to steer the cells. The two rows of stiff hairs cause a reversal of the flagellum thrust. Water is propelled along the flagellum from the tip to the base, so that the cell is towed forward in the direction of the flagellum (Figure 2.59)

FIGURE 2.59 Swimming pattern of Ochromonas danica.
In desmokont dinoflagellates such as
Prorocentrum sp., the longitudinal flagellum, which extends apically, beats with an anterior-to-posterior whipping action, generating a wave in a tip-to-base mode. The second flagellum, perpendicular to the first, is coiled and attached to the cell body except for the tip, which beats in a whiplash motion, while the attached part undulates (Figure 2.60). In dinokont dinoflagellates, such as
Peridinium sp. or
Gymnodinium sp., the two flagella emerge at the intersection of the cingulum (transverse furrow) and sulcus (longitudinal sulcus). The longitudinal flagellum extends apically running in the sulcus and is the propelling and steering flagellum, while the ribbon-shaped transverse flagellum is coiled, lies perpendicular to the first and runs around the cell in the cingulum. It is thought to be responsible for driving the cell forward and it also brings about rotation. The longitudinal flagellum beats with a planar waveform, which contributes to forward movement. The longitudinal flagellum can also reverse the swimming direction: it stops beating, points in a different direction by bending, and then resumes beating. This steering ability is related to change in orientation of basal bodies and contraction of the structures associated to the axoneme. In the transverse flagellum, a spiral wave generated in a base-to-tip mode is propagated along the axoneme, bringing about backward thrust and rotation at the same time (Figure 2.61).
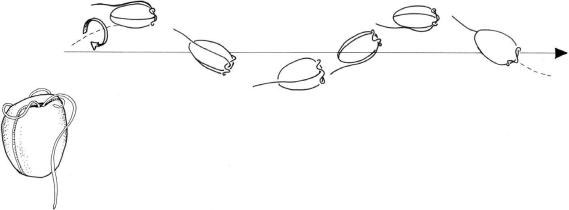
FIGURE 2.60 A desmokont dinoflagellate (Prorocentrum sp.) and its swimming pattern.
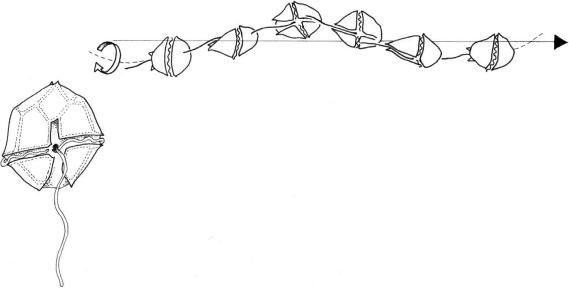
FIGURE 2.61 A dinokont dinoflagellate (Peridinium sp.) and its swimming pattern
As described earlier, the emergent flagellum of
Euglena sp. (Euglenophyta), bears simple hairs 3–4 mm long. These long hairs are arranged in tufts of three to four and form a single row that runs along the flagellum spirally with a low pitch. The flagellar hairs increase the thrust of the flagellum against the surrounding water. During swimming the long flagellum trails beside the cell body and performs helical waves, generated in a base-to-tip mode (Figure 2.62). A peculiar swimming pattern is present in the ovoid zoospores of
Chlorarachnion reptans and
Bigelowiella natans (Chlorarachniophyta), which bear a single flagellum inserted a little below the
cell apex. This flagellum bears very delicate hairs markedly different from the tubular hairs of
Heterokontophyta. During swimming the flagellum wraps back around the cell in a downward
spiral, lying in a groove along the cell body. The cells rotate around the longitudinal axis during
swimming and the anterior or posterior end of the cell moves in either narrow or wide helical
path which appears as a side-to-side roking or wobbling (Figure 2.63).

FIGURE 2.62 Swimming pattern of Euglena gracilis.
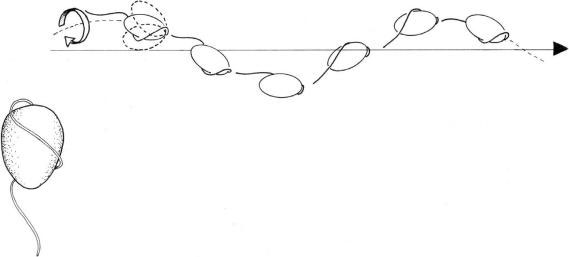
FIGURE 2.63 Swimming pattern of Bigelowiella sp.
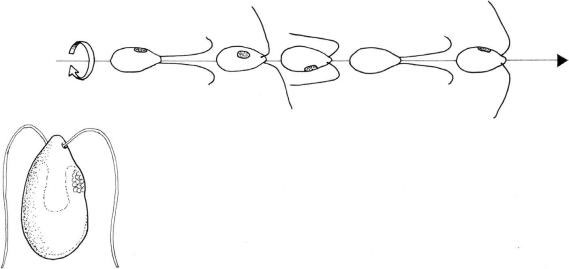
FIGURE 2.64 Swimming pattern of isokont biflagellate algae (Dunaliella salina).
In isokont biflagellate algae such as
Chlamydomonas or
Dunaliella (Chlorophyta), during the effective stroke the flagella bend only at the base, push more water backwards than adhereing to them during the forward recovery stroke, thus bringing about net forward movement. While swimming these cells also rotate. Speed ranging from 100 to 200 µm sec
-1 can be reached by these cells during forward swimming. Backward swimming is also possible, during which the flagella perform undulatory movement (Figure 2.64).

FIGURE 2.64 Swimming pattern of isokont biflagellate algae (Dunaliella salina).
An interesting question is why the algae swim. All algae in an aquatic environment have a need
to exchange molecules such as O
2, CO
2, and NH
3 with environment. As all solid boundaries in a liquid medium have associated with them a boundary layer in which water movement is reduced (due to the no-slip boundary), this layer will impede the nutrient uptake of the organisms by creating a small depleted layer around them. Turbulence is very ineffective in transporting nutrients towards such small organisms as the smallest length scale of turbulent eddies are of the order of several millimeters. Therefore, algae must rely on molecular diffusion to overcome the nutrient gradient across the boundary layer. Diffusion, that is the slow mixing caused by the random motion of molecules, is important in the world of low Reynolds number, because here stirring is not any good. The alga’s problem is not its energy supply; its problem is its environment. At low Reynolds number you cannot shake off your environment. If you move, you take it along; it only gradually falls behind.
Algae use their motility (be it sinking or swimming) to generate movement relative to the water
and hence replenish the boundary layer with nutrients. Depending on the size of the organism, the
motive for swimming must differ, however, because its effects differ significantly. For small algae
in the 1–10 µm range, diffusion is about 100 times more effective in supplying nutrients than movement. This is often expressed as the Sherwood number (
S):
where
L is the distance over which the nutrient is to be transported, u the water velocity, and
D the diffusion constant.
For scale of the order of 1 µm the ratio is ≈10
-2. Diffusion is about 100 times faster than movement. Hence, in this world of low Reynolds numbers, nothing is gained by trying to reduce the diffusion barrier by generating turbulent advection. In this context the only possible advantage to the alga of undertaking locomotion is that it might encounter nutrients in a higher concentration. For this purpose, a helical swimming path is more useful than a straight one inspite of the longer distance for the same displacement. This is because a helical swimming path enables the detection of three-dimensional component of a gradient, whereas the straight path allows detection of only one dimension.
Purcell (1977) summarized it by saying that the organism does not move like a cow that is
grazing on pasture, it moves to find greener pasture.
Only the species that swim very fast such as the dinoflagellates (about 500 µm sec
-1) can overcome the diffusion limitation. This high velocity should be related to the effective increase in the probability to catch more preys and therefore to the heterotrophy metabolism of the algal species.











