Radiant Flux Density (Irradiance and Radiant Exitance)
There are two possible conditions. The flux can be arriving at the surface in which case the radiant flux density is referred to as irradiance. Irradiance is defined as:
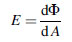 (5.9)
(5.9)where Φ is the radiant flux arriving at the infinitesimal area dA.
The flux can also be leaving the surface due to emission or reflection. The radiant flux density is then referred to as radiant exitance. As with irradiance, the flux can leave in any direction above the surface. The definition of radiant exitance is:
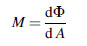 (5.10)
(5.10)where Φ is the radiant flux leaving the infinitesimal area dA.
Spectral radiant flux density is radiant flux per unit wavelength interval at wavelength λ. When the radiant flux is arriving at the surface, it is called spectral irradiance and is defined as:
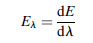 (5.11)
(5.11)When the radiant flux is leaving the surface, it is called spectral radiant exitance, and is defined as:
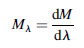 (5.12)
(5.12)Spectral radiant flux density is measured in watts per square meter per nanometer (W m-2 nm-1).
Imagine a ray of light arriving at or leaving a point on a surface in a given direction. Radiance is simply the amount of radiant flux contained in this ray (a cone of solid angle dω). If the ray intersects a surface at an angle θ with the normal to that surface, and the area of intersection with the surface has an infinitesimal cross-sectional area dA, the cross-sectional area of the ray is dAcos θ. The radiance of this ray is:
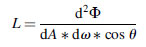 (5.13)
(5.13)Radiance is measured in watts per square meter per steradian (W m-2 sr-1).
Unlike radiant flux density, the definition of radiance does not distinguish between flux arriving at or leaving a surface.
The irradiance, E, at any distance from a uniform extended area source, is related to the radiance, L, of the source by the following the relationship, which depends only on the subtended central viewing angle, θ, of the radiance detector:
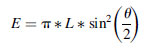 (5.14)
(5.14)Radiance is independent of distance for an extended area source, because the sampled area increases with distance, cancelling inverse square losses. The inverse square law defines the relationship between the irradiance from a point source and distance (d). It states that the intensity per unit area varies in inverse proportion to the square of the distance. In other words, if you measure 16 W m-2 at 1 m, you will measure 4 W m-2 at 2 m, and can calculate the irradiance at any other distance. An alternate form is often more convenient:
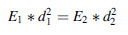 (5.15)
(5.15)Spectral radiance is the radiance per unit wavelength interval at wavelength λ. It is defined as:
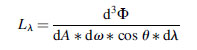 (5.16)
(5.16)and is measured in watts per square meter per steradian per nanometer (W m-2 sr-1 nm-1).
RADIANT INTENSITY
We can imagine a small point source of light that emits radiant flux in every direction. The amount of radiant flux emitted in a given direction can be represented by a ray of light contained in an elemental cone. This gives us the definition of radiant intensity:
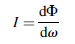 (5.17)
(5.17)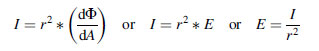 (5.18)
(5.18)where the infinitesimal surface area dA is on the surface of a sphere centered on the source and at a distance r from the source and E is the irradiance of that surface. More generally, the radiant flux will intercept dA at an angle θ from the surface normal. This gives us the inverse square law for point sources:
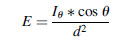 (5.19)
(5.19)Radiant intensity is measured in watts per steradian (W sr-1 ). Combining the definitions of radiance [Equation (5.13)] and radiant intensity [Equation (5.17)] gives us an alternative definition of radiance:
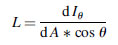 (5.20)
(5.20)where dIθ is the infinitesimal intensity of the point source in the θ direction with the surface normal.
Spectral radiant intensity is radiant intensity per unit wavelength interval at wavelength λ. It is defined as:
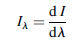 (5.21)
(5.21)and is measured in watts per steradian per nanometer (W sr-1 nm-1).





