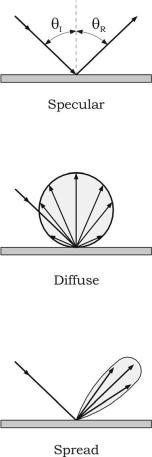
Reflection
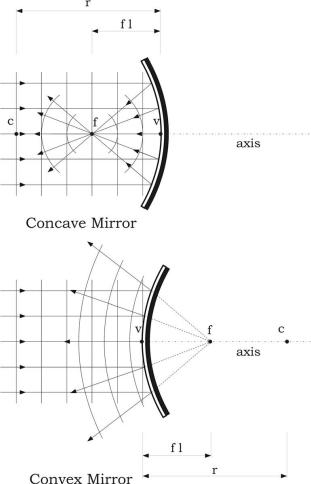
Now we will turn attention to the topic of curved mirrors, and specifically curved mirrors that have the shape of spheres, the spherical mirrors. Spherical mirrors can be thought of as a portion of a sphere that was sliced away and then silvered on one of the sides to form a reflecting surface. Concave mirrors were silvered on the inside of the sphere and convex mirrors were silvered on the outside of the sphere (Figure 5.6). If a concave mirror were thought of as being a slice of a sphere, then there would be a line passing through the center of the sphere and attaching to the mirror in the exact center of the mirror. This line is known as the principal axis. The center of sphere from which the mirror was sliced is known as the center of curvature of the mirror. The point on the mirror’s surface where the principal axis meets the mirror is known as the vertex. The vertex is the geometric center of the mirror. Midway between the vertex and the center of curvature is the focal point.
Unlike concave mirror, a convex mirror can be described as a spherical mirror with silver on the outside of the sphere. In convex mirrors, the focal point is located behind the convex mirror, and such a mirror is said to have a negative focal length value. A convex mirror is sometimes referred to as a diverging mirror due to its ability to take light from a point and diverge it. Any incident ray traveling parallel to the principal axis on the way to a convex mirror will reflect in a manner that its extension will pass through the focal point. Any incident ray traveling towards a convex mirror such that its extension passes through the focal point will reflect and travel parallel to the principal axis.
Refraction results when light is scattered in the same direction as that of incident light but passing between dissimilar materials, the rays bend and change velocity slightly. Refraction is dependent on two factors: the incident angle θ, that is, the angle between the incident light and the normal to the surface, and the refractive index, n of the material, defined as the ratio between the velocity of the wave in vacuum (cv) and the velocity of the wave in the medium (cs),
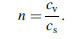 (5.2)
(5.2)The refraction results in the following relationship
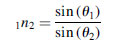 (5.3)
(5.3)where 1n2 is the refracting index in passing from Medium 1 to Medium 2 and θ1 and θ2 are the angles made between the direction of the propagated waves and the normal to the surface separating the two media.

FIGURE 5.7 Refraction of a light ray passing from a medium with lower refraction index (air) to a medium θ1, angle of incidence and θ2, angle of refraction.

FIGURE 5.7 Refraction of a light ray passing from a medium with lower refraction index (air) to a medium θ1, angle of incidence and θ2, angle of refraction.
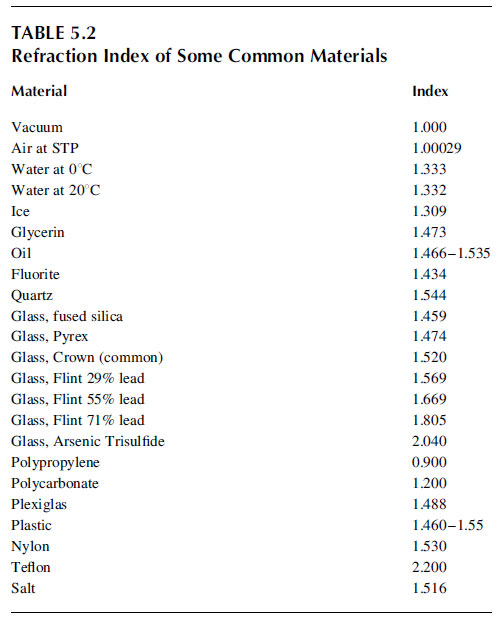
The index of refraction decreases with increasing the wavelength. This angular dispersion causes blue light to refract more than red, causing rainbows and prisms to separate the spectrum (dispersion). Table 5.2 shows the refraction index of some common materials.
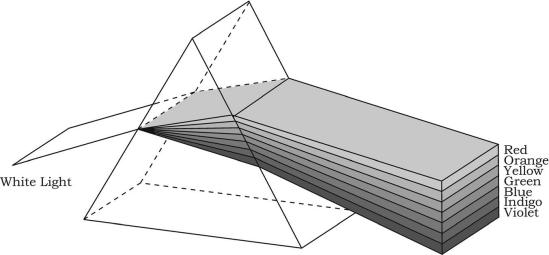
FIGURE 5.8 Dispersion of white light through a prism: the red portion of the spectrum deviates less than the violet from the direction of propagation of white light.
Dispersion is a phenomenon that causes the separation of a light into components with different wavelenghts, due to their different velocities in a medium other than vacuum. As a consequence, the white light traveling through a triangular prism is separated into its color components, the spectrum of light. The red portion of the spectrum deviates less than the violet from the direction of propagation of the white light (Figure 5.8).

FIGURE 5.8 Dispersion of white light through a prism: the red portion of the spectrum deviates less than the violet from the direction of propagation of white light.
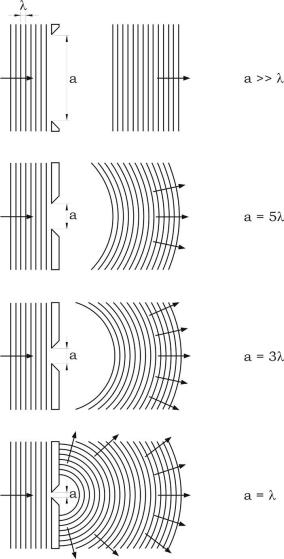
FIGURE 5.9 Diffraction of light from different width aperture; the effect increases with decreasing aperture width.
Light waves change the progagation direction when they encounter an obstruction or edge, such as a narrow aperture or slit (Figure 5.9). Diffraction depends on both wavelength of incoming radiation (λ) and obstruction or edge dimensions (a). It is negligible when a/λ is sufficiently large, and becomes more and more important when the ratio tends to zero. This effect is almost absent in most optical systems, such as photographic and video cameras, with a large a/λ; but it is very important in all microscopes, where diffraction limits the resolution that microscope can ultimately achieve (a/λ tends to zero). The resolution is the smallest distance between two points to discriminate them as separate.