Lifting the Fog: Image Restoration by Deconvolution
Deconvolution is a data processing technique that is very widely used in science and engineering. Biologists first applied this method to fluorescence microscopy in the early 1980s (Agard, 1984), but it was already in common use by astronomers for sharpening images acquired using telescopes. The term deconvolution is derived from the fact that it reverses the distortion (convolution) of data introduced by a recording system, such as a microscope when it forms an image of the specimen. Any microscope image of a fluorescent specimen can, in principle, be deconvolved after acquisition in order to improve contrast and resolution. The most common application in biology is for deblurring images acquired as three-dimensional (3D) image stacks using a wide-field fluorescence microscope, where each image includes considerable out-of-focus light or blur originating from regions of the specimen above and below the plane of focus. In essence, deconvolution techniques use information describing how the microscope produces a blurred image in the first place as the basis for a mathematical transformation that refocuses or sharpens the image. Deconvolution of wide-field data can provide results resembling the blur-free "optical sectioning" achieved with confocal microscopes, which remove the out-of-focus light optically before image acquisition by placing a pinhole in the appropriate position in the light path. Deconvolution is also applicable to confocal or multiphoton images as they too involve a convolution of data and, in practice, rarely exclude all out-of-focus information. The best deconvolution techniques attempt to correctly reassign each photon of the out-of-focus light from the blurred optical sections being processed to their points of origin within the image state.
This technical guide is intended both for those researchers who are completely new to the method and for those who use deconvolution, but would like a better appreciation of how the method works and the present state of the art. We will first briefly explain the principles of deconvolution and then describe the different types of deconvolution methods currently available. Next we discuss practical considerations and limitations in applying the techniques. Finally, we describe improved deconvolution algorithms, which are currently being developed.
The magnified image of a specimen observed by eye or a digital camera mounted on a microscope is not a perfect representation of the specimen. The image is blurred or convolved by the microscope optics and some information is lost (Fig. 1A). This is an inevitable consequence of how objective lenses work and there are no simple ways round the problem (Hecht, 2002). The nature of image convolution in fluorescence microscopy is appreciated most easily by viewing small spherical fluorescent beads (with diameters in the order of hundreds of nanometers; Figs. 1B-1D). When the beads used are smaller than the smallest detail that the optics can resolve (i.e., subresolution, 50 to 200nm), they form effective single point sources of light and the image resulting from a single bead is known as the point spread function (PSF), being a record of how much the microscope has spread or blurred a single point while imaging it (Jonkman et al., 2003; Figs. 1B-1D). Such images consist of a series of concentric rings in three dimensions (so-called airy rings) of out-of-focus light around points of light (Figs. 1B and 2A). The PSF is a three-dimensional function, describing how the image of a subresolution point is blurred in the z dimension as well as in x and y, and it varies between different objectives, those with higher numerical apertures giving less blurring (Figs. 1B-1D). Wide-field, confocal, and multiphoton imaging configurations all have their own characteristic PSFs. A biological specimen may be thought of as a collection of subresolution points, each of which is convolved by the objective's PSF independently. Mathematically, convolution involves replacing each point in the specimen by a point spread function during the process of image formation. It is the combination of out-of-focus light from these overlapping PSFs in and beyond the plane of focus that leads to the familiar blur in widefield fluorescence images (Figs. 3A and 4A).
 |
| FIGURE 1 Convolution, deconvolution, and the point spread function (PSF). (A) Interpretive diagram of the principles of convolution and deconvolution based upon a simple spherical object. (B-D) Wide-field fluorescence PSFs obtained by imaging 100-nm fluorescent beads (excitation 520nm; emission 617nm) with a ×40/NA 0.85 dry objective and with a ×40/NA 1.35 oil immersion with adjustable collar set at NA 1.35 and NA 0.85. Images shown are single median x, z planes from 3D data sets, step size 0.1 µm. (Inset) An x, y view 20 µm from the centre. Deterioration of the PSF from C to D is a consequence of mismatch of the immersion oil refractive index with the reduced numerical aperture set. Resolution in z depends upon both RI and NA. |
 |
| FIGURE 2 (A) Three-dimensional (x, y, z) view of a wide-field fluorescence point spread function. For clarity, the volume representation is shown as a negative image. (B) Two different representations of the Fourier transform of a PSF-an optical transfer function (OTF). In the OTF, frequency information is plotted in "k space" or reciprocal space (where kz is reciprocally related to z and kr to x and y in real space, see Technical Summary 2). OTFs are often averaged radially over x, y, hence the axis kr. The area covered by the OTF corresponds to the frequency information collected by the optics. The "missing cone" region (arrows) corresponds to lost frequencies due to the limited size of the objective pupil, a consequence of this being the far greater blurring of an object along the z axis than in x and y. |
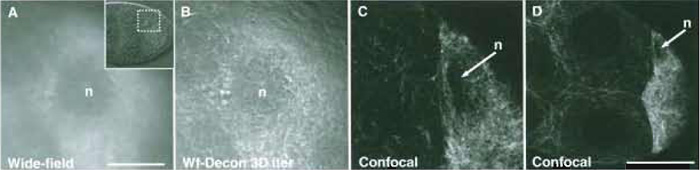 |
| FIGURE 3 Comparison of wide-field and confocal imaging of living Drosophila egg chambers (stage 8) expressing Tau-GFP localised to the tubulin cytoskeleton. (A) Wide-field image of the area surrounding the oocyte nucleus (see insert: DIC image of the egg chamber). The image required 200ms exposure. (B) Image A after 3D iterative deconvolution using the Applied Precision Resolve 3D algorithm (softWoRx, API). (C) Point scanning confocal optical section of a similar egg chamber, which took 2 s to collect. (D) Wider view of the confocal image of the egg chamber from C. All images were collected with ×60/1.2 NA water immersion objectives. Scale bars: 100µm (A-C) and 50µm (D). The oocyte nucleus (n) is indicated in each case. |
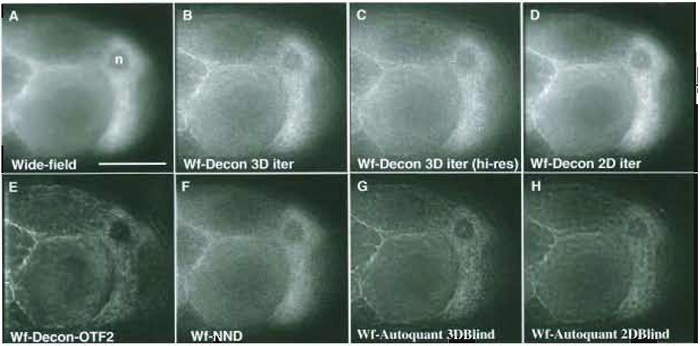 |
| FIGURE 4 Comparing the results of different deconvolution methods on a challenging 3D (60 image) wide-field data set of a Drosophila egg chamber (z-step 0.2µm, x, y pixel size 0.212µm; a ×60 1.2 NA water objective). (A) Single unprocessed wide-field image. (B) The corresponding image plane after 3D iterative, constrained deconvolution of the data set (softWoRx, API: empirical PSF). (C) Deconvolution as in B using a second 60 image 3D data set of the same tissue collected at an x, y pixel size of 0.106gm--higher sampling rate. (D) Two-dimensional iterative constrained deconvolution of the first image data set (softWoRx, API: empirical PSF). Each z plane is deconvolved independently as if it were part of a time-series data set. (E) Deconvolution as in B but using a different PSF (OTF) and more severe smoothing. (F) Using the "nearest neighbours" deconvolution algorithm (softWoRx, API). (G) Using the 3D iterative, "adaptive blind" deconvolution algorithm (Autodeblur, Autoquant-10 iterations; low noise; no spherical aberration; recommended expert settings). (H) Using the 2D iterative, adaptive blind deconvolution algorithm (Autodeblur, Autoquant-15 iterations; low noise; no spherical aberration; recommended expert settings). Scale as for Fig. 3D. Raw data were 12 bit saved as 16 bit; the images shown are 8 bit; with contrast stretched to fill the full dynamic range. |
III. DECONVOLUTION, DEBLURRING, AND IMAGE RESTORATION
Given the raw image and the PSF for the imaging system it should, in principle, be possible to reverse the convolution of an object by the microscope mathematically, according to a simple relationship-the so-called "linear inverse filter" (Technical Summary 1). However, in practice, simple reversal of convolution is not possible, primarily because of the confounding effect of noise in image data, which becomes amplified during this process (Technical Summary 1). Several fundamentally different deconvolution approaches of varying complexity have been developed to overcome this problem (see Table I; Agard, 1984; Agard et al., 1989; Holmes et al., 1995; van Kempen et al., 1997).
Technical Summary 1: Convolution Theory and Fourier Space
Convolution refers to the effect that the microscope optics has in forming the image of an object viewed through the microscope. the microscope image is the result of the convolution (symbolised by
| Microscope image = object |
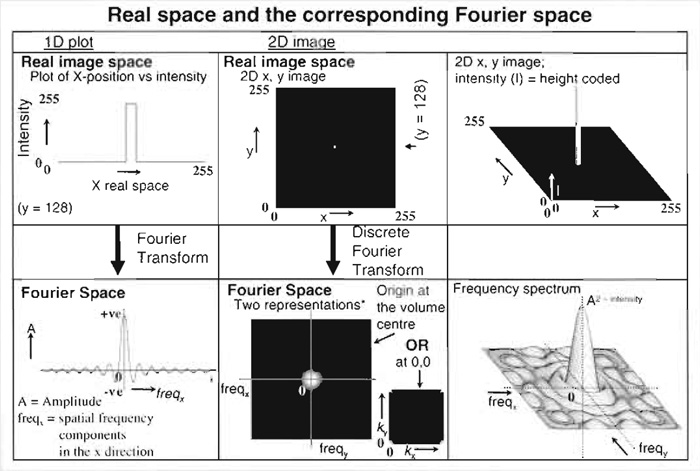
In theory, determing what the object should look like, given the microscope image and the PSF, simply requires reversal of this convolution. Performing this calculation using image data directly (known as calculating in "real space") is computationally very time-consuming. This limitation may be overcome by carrying out calculation in "Fourier space" by computing the Fourier transform (FT) of both image data and the PSF (see Technical Summary 2). The Fourier-transformed PSF is also known as an optical transfer function (OTF). In Fourier space, the convolution relationship described earlier becomes a simple multiplication:
| FT (microscope image) = FT (object) × FT (PSF), or equivalently |
| FT (microscope image) = FT (object) × OTF (Van der Voort and Hell) |
Deconvolution on the basis of the aforementioned equation is known as a simple linear inverse filter (Table I). However, the Simple linear inverse filter is of very little practical use, as the relationship between image and object is invalidated by noise in the collected image. The simple linear inverse filter does, however, provide the theoretical basis for more complex deconvolution algorithms that take account of real imaging situation (Hiraoka et al., 1990).
There is considerable confusion caused by the existence of different names for deconvolution algorithms due to the history of development of this method (Agard, 1989; van Kempen et al., 1997). Currently, only a few algorithms are routinely employed in biological image processing (Table I). In an article by Wallance et al. (2001), algorithms are classified info (1) "deblurring" methods (Table I), which are said to act two-dimensionally, on one z plane at a time, and (2) "image restoration" or "true deconvolution" methods, which act in a truly three-dimensional way on all planes simultaneously. IN general, deblurring methods may be useful for a rapid qualitative improvement in image contrast, e.g., to aid data screening (Fig. 3F, nearest neighbour deconvolution). However, the most powerful algorithms are the constrained iterative procedures of the second class:considered as the method of choice for quality 3D data processing, these will be the focus of the remainder of this article. Within the family of constrained iterative approaches, different algorithms vary in the way noise is modelled and how PSF information is dealt with (Table I; Agard et al., 1989; Holmes et al., 1995; van Kempen et al., 1997).
| TABLE I Deconvolution Algorithms Used in Biological Fluorescence Image Processing a | ||
| Algorithm/product name b | Features | |
| Deblurring class Subtractive | Widely available in image processing software as "nearest neighbours" or "no neighbours" processing. (e.g., Metamorph, Universal Imaging; Autodeblur, Autoquant) | Works on the basis that most of the out-of-focus blur originates in the neighbouring planes in z (when sampling at approximately the z resolution). The nearest z sections above and below the section being corrected are blurred with a filter and these blurred images are then subtracted from the plane of interest to give the deblurred section. "No neighbours" extrapolates only from a single plane.
|
| Image restoration class Linear inverse filter | For example, the Tikhonov- Miller filter used in analySIS | The simplistic approach of reversing convolution by the optics. Does not take account of the effects of noise. Often used as the "first guess" for iterative deconvolution. Still a true 3D method requiring a PSF, which attempts to reassign out of focus information to its point of origin.
|
| Regularised inverse filter | For example, the regularised Wiener filter. Found in several applications, e.g., DeconvolveJ, NIH image,cAutodeblur-inverse filter from Autoquant and Axio Vision 3D-Deconvolution from Carl Zeiss | A refinement of the above employing regularisation so that the deconvolution solutions are physically realistic and artifacts are suppressed. Regularisation involves limiting the possible solutions that are accepted in accordance with certain assumptions made a priori about the object, such as the degree of smoothness, essential when dealing with real, noisy data. Limiting the contribution of noise by regularisation comes at the expense of resolution, and to optimise this trade-off between image sharpness and noise amplification, different values of the regularisation parameter must be assessed. |
| Constrained Iterative Additive (Gaussian) noise model | For example, the modified Jansson van Cittert algorithm (Agard et al., 1989) implemented in modified form in soflWoRx from API | A further refinement on the aforementioned; an additional positivity constraint is applied that restricts output image intensities to be positive (see main text).
|
| Constrained Iterative Maximum Likelihood estimation (Poisson noise model) | For example, the Richardson- Lucy algorithm implemented in Huygens Essential from Scientific Volume Imaging. Also AxioVision 3D- Deconvolution from Carl Zeiss | A variant of the constrained, iterative algorithms that assumes a Poisson model to quantify the noise present during imaging. Huygens essential uses the classical maximum likelihood estimation method and either optimised empirical or theoretical PSFs.
|
| Constrained Iterative Adaptive Blind deconvolution | Includes the EM-MLE (expectation minimisation algorithm) of Autoquant's Autodeblur-2D and 3D blind deconvolution options | Blind deconvolution is also iterative and constrained but it determines an estimate of both the object and the PSF of the imaging system based upon raw image data and certain a priori assumptions about the PSF. These algorithms also assume a Poisson model of noise in the image.
|
| a Represents a summary of commonly used algorithms and is not intended to be exhaustive. | ||
| b These products may be sold (under license) by other agents. | ||
| c National Institute of Health Image-J software is free to download from http://rsb.info.nih.gov/ij. | ||
The constrained iterative deconvolution approach (Agard, 1984; Agard et al., 1989) is truly restorative, in that it attempts to reassign (put back) the out-of-focus light to its expected point of origin rather than simply subtract it from the imge as with the deblurring methods (Table I; Figs. 3 and 4). This not only increases the brightness of features in the object thus improving signal-to-noise levels, but also improves contrast and apparent resolution. Furthermore, these algorithms are capable, under ideal circumstances, of deconvolution solutions with so-called superresolution along the Z axis-the recovery of detail lost from the image by the convolution of the optics (i.e., beyond diffraction-limited resolution). This phenomenon is usually explained in terms of "the recovery of lost spatial frequencies" or the "missing cone" of z information (Hiraoka et al., 1990; Goodman, 1996), a reference to the shape of the PSF in Fourier space (Fig. 2B; Technical Summary 2).
Fourirer transformation represents an image in terms of the spatial frwquency information it contains. sharp edges or fine details correspond to high spatial frequencies; large areas of slowly changing intensity have low spatial frequencies. The entire image can be considered to be the result of the combination of a set of complex "waves." The summation of these waves to create the image is described mathematically as the three-dimensional integral of many simple sinusoidal wave functions, each having specific frequencies, phases, and amplitudes. The Fourier transform of the image (a "discrete Fourier transforms" in the case of image data) is a plot of the frequency information present in the real space image, each point representing a particular spatial frequency (see figure below; Hecht, 2002).
- Fourier transformation is used in deconvolution processing simply because the convoluation calculation is much faster in Fourier space (Frequencyx, Frequencyy, Frequencyz) than in real space x,y,z (Van der Voort and Hell, 1997).
- In Fourier space, the dimensions along the axes are spatial frequency. These reciprocal space coordinates do not map directly to x,y,z positions in real space, but are related to them reciprocally, i.e., things that are closer together in real space (fine details) give high spatial frequency componentsthat are further from the mathematical origin of the Fourier transform in Fourier space and vice versa. For this reason, Fourier space is often reffered to as "reciprocal space." Amplitudes in a real space image result from the summed amplitudes of each spatial frequency component (effectively how often a particular frequency occurs).
The name used for the "constrained iterative" class of deconvolution refers to the two critical features that define it: "constrained" and "itenative." The term "constrained" refers to the use of the "Positivity constraint." "Iterative" refers to the way which these algorithms are implemented by repeated cycles of comparison and revision.
A consequence of all this processing is that implementation is very computationally demanding and so potentially slow. However, modern computers have become so fast and relatively inexpensive that a large deconvolution task, such as a stack of 64 z sections, each of 512 × 512 pixels, can be completed in a few minutes.
C. Using Deconvolution
To achieve the best image quality from a wide field imaging system (i.e., resulting in features sharply defined by high contrast and with a resolution is almost indispensable.
Wide-field deconvolution can provide a similar degree of reduction in out-of-focus blur as does confocal microscopy, but without the elimination and loss of signal associated with passing the emitted light through a confocal pinhole (Swedlow et al., 2002; pawley and czymmek, 1997). Aided by the high quantum efficiency (QE) charge-coupled device (CCD) detectors used (Amos, 2000), wide field is both fast and sensitive compared to point scanning confocal imaging, making it especially useful for rapid imaging of labile, dynamic processes in live material (Periasamy et al., 1999; Wallace et al., 2001; Swedlow et al., 2002).
Deconvolution and confocal imaging are by no means mutually exclusive: confocal imaging can nearly always benefit from the improvements in contrast, signal-to-noise ratio, and resolution afforded by restorative deconvolution methods (Wiegand et al., 2003). Furthermore, while excluded photons cannot be restored, the application of deconvolution to confocal images does allow the confocal pinhole to be opened slightly during imaging, sacrificing confocality but increasing signal and reducing spherical aberration effects (Pawley, 1995). The brighter but more blurry images are then restored by deconvolution. This is particularly helpful where SA precludes the use of small pinhole settings, e.g., when imaging deep within a specimen (>10µm). However, one of the biggest limitations when deconvolving confocal images is that they tend to be very noisy because of the low signal available due to the low light throughput and low quantum efficiency of photon multipliers used as detectors in confocal imaging. This problem can best be dealt with either by averaging frames or decreasing scan rate, both at the expense of speed, rather than by increasing the gain on the PMT (which merely introduces more noise). The Huygens Professional software from scientific volume imaging (SVI) addresses the noise content of raw data and makes use of this information during restoration. Another potential problem with deconvolution of laser scanning confocal images is that the pinhole size affects the point spread function. SVI's Huygens deconvolution software or Autoquant's Autodeblur program both offer solutions to this problem in that they have options to take account of the effect of the confocal pinhole on the PSF.
While true deconvolution is a spatial 3D (x, y, z) phenomenon, often the need is to process tme-lapse data (x, y, and time). Algorithms exist that are specifically designed to deal with such data (see later for details); however, deconvolution with only spatial 2D data is necessarily not as effective as with a full 3D stack of z sections, as it lacks information to take proper account of distortion in the z dimension. It is also important to note that deconvolution cannot take account of "motion blur" during image capture so suitably short exposure times are essential.
Deconvolution, particularly the more advanced approaches, is implemented through a software package where the algorithm is generally assisted by data correction before and noise reduction steps both before and between iterations. With a given deconvolution package, the quality of results obtained will depend foremost upon the quality of raw image data and upon the accuracy of PSF data. Next in importance is the algorithm used and how well it is implemented: noise handling, background or dark signal correction, the initial guess, the regularisation parameter, and filtering and smoothing steps. As different settings, algorithms, or packages may have varying success with different data, it is invaluable to test different programs to understand how a program behaves with your own raw data (Fig. 4A-4H) and to pay close attention to software manufacturers' criteria for raw data and data collection.
A. Collection of Raw Image Data
The quality of raw data is arguably the most important determinant in obtaining good deconvolution results. Essentially, improving raw data involves improving the useful signal-to-noise ratio of images (Pawley, 1995). The most important factors relating to this are given in Technical Summary 3. In our experience, it is always easier to meet criteria for good imaging in fixed material than it is for living material where compromises must be made (Davis and parton, 2004).
Technical Summary 3: Data Collection Procedures
1. Use a correctly set up and aligned microscope with high-quality objective lenses, accurate z control (by Piezo focusing or motorised stage, Fig. 5), and low noise detectors of good dynamic range and high QE (proportion of photons arriving at the detector that go to produce an output signal).
 |
| FIGURE 5 Different approaches to z movement control. (A) An x,y,z motorised stage from the API Deltavision system. (B) A piezo z-drive nosepiece from Precision Instruments. Note that use of a nosepiece under an objective may alter its PSF. |
The quality of deconvolution is dependent upon correct positional information. Pixel sizes should be determined by accurate calibration of the image in x and y, and the z drive should be as precise and reproducible as possible. [For example, the nanomovers offered by applied Precision Inc. (API) for their Deltnvision system have 4nm precision and 30nm repeatability. Pifoc drives supplied by Precision Instruments are more accurate and reproducible, depending on the speed of movement and time allowed to settle (Fig. 5), but alter the point spread function and can only be mounted on objection at a time.]
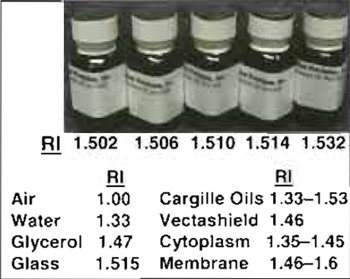 |
| FIGURE 6 Cargille immersion oils of varying refractive index (RI) and several useful RI values. Note that dilutions of glycerol (80 to 40%) give RI of 1.446 to 1.391. |
In general, current deconvolution methods are poor at taking account of aberrations in the imaging optics or distortions produced by imaging in thick specimens (primarily SA) or by motion blur. Sample preparation using appropriate mounting media to match the refractive index (RI) of the specimen and the use of correct immersion medium for the objective used (dry, oil, water, or glycerol) can reduce spherical aberration. It is also important to use the correct coverslip thickness or correction collar settingfor the objective (default 0.17mm; #1.5) and to ensure that as far as possible the specimen is immediately adjacent to the coverslip. Imaging deep into specimens (>10 µm) increases SA, which can be peartly corrected using objectives with correction collars or by using immersion oils of higher than normal RI (Fig. 6; Davis, 2000).
2. To realise the optical resolution of your imaging system, it is important to follow the Nyquist sampling rule by using a pixel size in the electronic imaging device at least two times smaller (ideally, a minimum 2.3 times) than the expected optical resolution in x,y, and z (Pawley, 1995; Jonkman et al., 2003). It is possible to determine the theoretical optical resolution based upon the numerical aperture of the objective and emission wavelength using the equation below. The values obtained should be used as an estimate on which to base the digital sampling size. however, in reality it may benifit the final result to make a small sacrifice in the sampling rate by binning pixels on a CCD readout to boost signal-to-noise ratio, increase imaging speed, or avoid flurochome photobleaching. Figure 4C shows deconvolution result improvement with better x,y spatial sampling (0.106 µm pixel) compared to fig. 4B (0.212 µm), despite the lower fluorescence signal.
Calculation to determine theoretical resolution limits:
| Lateral (XY) resolution = 0.61 * wavelengthemision/numerical apertureobjective |
| Axial (Z) resolution = 2 * wavelengthem * refractive index/(numerical apertureobj)2 |
(refractive index in this case refers to the specimen immersion medium RI)
3. In general, it is not advisable to collect Z planes so far below or above the best focus that only blur is seen, as you only end up bleaching the sample.
(S/N = n/√n or simply √n, where n may be approximated as the image signal) is the fundamental limitation in S/N. As the number of photons detected increases, the signal-to-noise ratio improves according to the poisson statistics of photon detection. The signal should not, of course, be so high as to saturate the detector. both the Huygens (SVI) and Autodeblur (Autoquant) programs make use of "roughness penalty factors," which, unlike smoothing filters, can be set by the user to constrain their deconvolved solutions to reduce noise while preserving edge features.
The detector should have good dynamic range, high quantum efficiency (QE), low dark signal, and low readout noise (Amos, 2000). When taking short exposures with CCD detectors, readout noise tends to be the most important source of detector noise, whereas when taking long exposure, dark current predominates.
Slow-scan cooled CCD detectors with low dark current and readout noise, reading out pixel intensities as 12-16 bit images (214 = 4096, 216 = 65,536 intensity levels), are used most commonly in wide-field fluorescence imaging systems. They can produce images with a large dynamic range (total intensity levels/intensity levels of noise) and favourable overall S/N ratio.
Confocal systems are less light efficient, and the images they produce are generally photon limited and most commonly recorded as only 8 bit data (=256 intensity levels). Therefore confocals are more prone to noise problems. Point scanning confocals use relatively low QE photomultipliers, whereas disc scanning systems use CCDs. Imaging only bright signals or averaging several frames to count more photons can help reduce such noise problems.
6. Intensity fluctuations due to light source flicker or bleaching during the collection of z sections or time series images have an adverse affect on deconvolution. Using stable power suppliers, regulatly changing mercury arc lamps, or measuring fluctuations and correcting collected data can help significantly (Delta Vision System, API). Bleaching may be reduced by the use of an antifade reagent, which are available commercially or can be home made. Some algorithms include bleaching correction based upon an expected theoretical rate of decline in fluorescence.
B. The PSF (and Its Fourier Transform the OTF)
In addition to optimising raw image quality, using the correct PSF for the image being deconvolved is fundamental to the final result, as one might expect from the convolution relationship discussed in detail earlier (Fig. 1; 4B compared to 4E). A PSF may be emoirical (i.e., measured; Hiraoka et al., 1990 but see Van der Voort and Strasters, 1995; Davis, 2000) or theoretical (calculated). The former is generally recorded by 3D imaging of subresolution beads using exactly the same optics as used to image the specimen, whereas the latter is generated by the software package used, after inputting the emission wave-length, objective lens details, and refractive index of the immersion medium and mounting medium (e.g., Huygens from SVI; Zeiss 3D Deconvolution Module from Zeiss; Autodeblur from Autoquant). Important considerations relating to PSFs are given in lechnical Summary 4.
Empirical PSFs
- if collected correctly, these have the greatest potential for high-quality deconvolution of images taken with high numerical aperture ienses. However, a poor empirical PSF is certainly worse than a theoretical one (Hiraoka et al., 1990).
- Are often collected at 488-nm excitation and 520-nm emission wavelengths. Software packages usually make adjustments when the actual imaging situation is at a different wavelength. Huygens (SVI) offers the possibility of multiwavelength PSF Processing as an aid to chromatic aberration correction in colocalisation.
- Experience reveals that collecting a PSF to match the true aberrated imaging situation in vivo (e.g., by injecting fluorescent beads into a cell or by mounting beads so that they are imaged through a particular depth of media of refractive index close to that of a cell) is less effective than using a PSF corresponding to optimal imaging conditiond and aspiring to match in vivo imaging conditions to that situation.
- Some software packages come with prerecorded optimised (e.g., averaged over many beads or "processed" by averaging, smoothing, or deconvolving) empirical OTF's for particular objectives, and using these is often preferable to collecting your own (e.g., API's softWoRx package; Fig. 2B). Huygens (SVI) permits optimisation of your own empirical PSF data by registering and averaging images of multiple beads and correcting for the fact that a bead is, in reality, not an infinitely small point source.
- In the case of objective lenses with numerical aperture collars, it may be necessary to collect specific PSFs for each setting of the collar (1C and 1D), similarly for different confocal pinhole apertures.
Theoretical PSFs
- These work well with low NA, low magnification objectives.
- They are usefully employed in some software packages for use with confocal (and MP) imaging, as they can be optimised for different confocal pinhole settings by calculation.
- "Blind deconvolution," Autoquant, Autideblur) offer an effective way to circumvent some of the issue mentioned earlier. Insted of using an empirical or calculated PSF, an estimate of the "true" PSF is generated iteratively from the image data itself at the same time as image restoration (Holmes et al., 1995).
- Adaptive blind deconvolution can be useful where a representative PSF is not easy to obtain, such as with confocal imaging using variable pinhole settings, multiphoton imaging, or imaging in the presence of SA.
- Adaptive blind deconvolution is not a perfect solution, as it is only an estimate determined on the basis of severe constraints imposed upon possible solutions.
Ultimately, it is necessary to determine by trial and error the approach that works best for any particular data type. In virtually all cases, the use of a signal PSF for an entire 3D image set is a compromise, especially with live material. Generally, the optical conditions vary between parts of the same image or at different z planes (i.e., the PSF itself varies spatially). However, most current algorithms assume a spatially invariant PSF to simplify processing (Hiraoka et al., 1990).
Advances in computer technology have had a great impact upon deconvolution, largely because of the computational demands of this approach (Holmes et al., 1995; Wallace et al., 2001). Be aware that with the requirements of deconvolution for multiple z planes and with CCD image detection noe able to generate 1024 × 1024 × 16 bit images many times a second, computer systems must deal with many gigabytes of information within relatively short periods of time. Implementation of deconvolution algorithms requires appropriate processor power and adequate data transfer, short-term storage, and archiving capabilities While in the past deconvolution required special high-performance workstations, dual processor personal computers with at least 1Gb of RAM, greater than 50Gb hard drives, CD, or DVD-R writers and network connection speeds of 100Mbit/s to 1Gbit/s are now standardly used for deconvolution. To increase the efficiency of a laboratory, it is desirable to have separate computers dedicated to image capture and image analysis. A high-quality properly set up monitor (24- or 32-bit colour; calibrated to set contrast and brightness) is necessary for viewing image data. Where many users are involved, it is desirable to have a rack-mounted cluster of many computers linked to a RAID disk (redundant array of independent discs), networked to stand-alone acquisition and processing stations for individual user access.
Deconvolution works best when imaging conditions are near optimal, which is possible for fixed material but rarely achieved in living specimens (Kam et al., 2000). If the raw images are poor, deconvolution can perform poorly or even produce artefacts that degrade the images. Visual assessment of the removal of out-of-focus blur is a useful guide of success, taking care to correctly set the brightness and contrast of the image display. Features should emerge sharpened with increased brightness after processing. However, as a general guide, you should only trust features observed in the deconvolved image when they are also present, however faintly, in the unprocessed original image. Comparison of the deconvolved results with images acquired by an independent technique, such as electron microscopy or confocal imaging, is also useful. Detailing deconvolution artefacts and their basis is beyond the scope of this article and are dealt with elsewhere (e.g., Wallace et al., 2001). In general, small punctate or ring-like features should be viewed with scepticism, while excessive noise suggests poor initial data or problems with the parameters used. If detail appears to be lost after processing, then initial background subtraction may have been too high or filtering and noise suppression steps too aggressive.
Quantitative positional and structural analysis, which is not so dependent upon absolute intensity values, including centroid determination, movement tracking, volume analysis, and colocalisation, have all been performed successfully on deconvolved data (e.g., Van Der Voort and Strasters, 1995; Wallace et al., 2001; Landmann, 2002; Wiegand et al., 2003; Macdougall et al., 2003). Where quantitative analysis is intended, it is essential to apply deconvolution systematically, with an understanding of possible artefacts and, if possible, with confirmation by an independent technique.
Improvement in the quality of the initial imaging is the most effective way to enhance deconvolution. For example, correct sampling, noise reduction, use of photon limited (rather than noise limited) detectors, precise and rapid piezo z movers, and better corrected objectives all help to improve the quality of imaging and hence the deconvolution result. However, advances are also being made in the quality of processing. Faster computers are allowing the use of increasingly more complex calculations within realistic timescales. More advanced deconvolution algorithms are being developed to deal with the poor signal to noise and with the aberrations associated with imaging in vivo (Holmes et al., 1995; Kam et al., 2000). Pupil functions, which are in use in astronomy, are beginning to be used in biology (Hanser et al., 2003) in order to correct for asymmetries in the PSF (current deconvolution algorithms assume that the PSF is radially symmetric in x and y and bilaterally symmetric in z). Iterative constrained algorithms aided by wavelet analysis may allow us to tackle situations of poor signal to noise and distorted PSF when imaging deep in vivo using confocal and multiphoton techniques (Boutet de Monvel, 2001; Gonzalez and Woods, 2002).
We thank John Sedat, Satoru Uzawa, Sebastian Haase, Lukman Winito, and Lin Shao (University of California San Francisco) and also Zvi Kam (Weizmann Institute of Science) for interesting discussions relating to deconvolution. We are also indebted to Jochen Arlt and the COSMIC imaging facility (Physics Department, University of Edinburgh) for invaluable technical advice and access to advanced imaging equipment and also to Simon Bullock, David Ish-Horowicz, Daniel Zicha, and Alastair Nicol (Cancer Research-UK, London) for allowing access to their imaging equipment and for the introduction to wavelet analysis. Thanks for technical advice must also go to the many contributors to the Confocal List (URL: http://listserv.acsu.buffalo.edu/cgi-bin/wa?S1=confocal); Carl Brown of Applied Precision Inc. (USA); Jonathan Girroir of AutoQuant Imaging (USA); and Rory R. Duncan, University of Edinburgh Medical School. We are grateful to Renald Delanoue, Veronique van De Bor, and Sabine Fischer-Parton (University of Edinburgh) for critical reading of the manuscript.
Andor Technology (EMCCD cameras) www.andor-tech.com
Applied Precision (Deltavision) www.api.com/lifescience/dv-technology.html
Autoquant (see education pages) www.aqi.com also www.leica.com
Carl Zeiss (3D Deconvolution) www.zeiss.co.uk (Axio Vision, 3D-Deconvolution)
Huygens (see essential user guide) www.svi.nl also www.bitplane.com and www.vaytek.com
Image J (FFTJ and Deconvolution-J) http://rsb.info.nih.gov/ij/plugins/fftj.html
Mathematica for wavelet analysis www.hallogram.com.mathematica.waveletexplorer/www.wolfram.com/products/ applications/wavelet /
Power Microscope On-line deconvolution www.powermicroscope.com
References
Agard, D. A. (1984). Optical sectioning microscopy: Cellular architecture in three dimensions. Ann. Rev. Biophys. Bioeng. 13, 191-219.
Agard, D. A., Hiraoka, Y., Shaw, P., and Sedat, J. W. (1989). Fluorescence microscopy in three dimensions. Methods Cell Biol. 30, 353-377.
Amos, W. B. (2000). Instruments for fluorescence imaging. In "Protein Localization by Fluorescence Microscopy" (V. J. Allan, ed.), pp. 67-108. OUP, Oxford.
Boutet de Monvel, J., Le Calvez, S., and Ulfendahl, M. (2001). Image restoration for confocal microscopy: Improving the limits of deconvolution, with application to the visualization of the mammalian hearing organ. Biophys. J. 80(5), 2455-2470.
Davis, I. (2000). Visualising fluorescence in Drosophila: Optimal detection in thick specimens. In "Protein Localisation by Fluorescence Microscopy: A Practical Approach" (V. J. Allan, ed.), pp. 131-162. OUP, Oxford.
Diaspro, A. (2001). "Confocal and Two-Photon Microscopy: Applications and Advances." Wiley-Liss, New York.
Gonzalez, R. C., and Woods, R. E. (2002). "Digital Image Processing," 2nd Ed. Addison-Wesley, San-Francisco.
Goodman J. W. (1996). "Introduction to Fourier Optics," Chap. 6. McGraw-Hill, New York.
Gusstafsson, M. G. L. (1999). Extended resolution fluorescence microscopy. Curr. Opin Struct. Biol. 9, 627-634.
Hanser, B. M., Gustafsson, M. G. L., Agard, D. A., and Sedat, J. W. (2003). Phase retrieval of high-numerical-aperture optical systems. Optics Lett. 28, 801-803.
Hecht, E. (2002). "Optics," 4th Ed., pp. 281-324 and 519-559. Addison Wesley, San Francisco.
Holmes J. H., Bhattacharyya, S., Cooper, J. A., Hanzel, D., Krishnamurthi, V., Lin, W., Roysam, B., Szarowski, D. H., and Turner, J. N. (1995). Light microscope images reconstructed by maximum likelihood deconvolution. In "The Handbook of Biological Confocal Microscopy" (J. B. Pawley, ed.), 2nd Ed., pp. 389-402. Plenum Press, New York.
Jonkman, J. E. N., Swoger, J., Kress, H., Rohrbach, A., and Stelzer E. H. K. (2003). Resolution in optical microscopy. Methods Enzymol. 360, 416-446.
Kam, Z., Hanser, B., Gustafsson, M. G. L., Agard, D. A., and Sedat, J. W. (2000). Computational adaptive optics for live threedimensional biological imaging. Proc. Natl. Acad. Sci. USA 98, 3790-3795.
Landmann, L. (2002). Deconvolution improves colocalisation analysis of multiple fluorochromes in 3D confocal data sets more than filtering techniques. J. Microsc. 208(2), 134-147.
MacDougall, N., Clark, A., MacDougall, E., and Davis, I. (2003). Drosophila gurken (TGFalpha) mRNA localises as particles that move within the oocyte in two dynein-dependent steps. Dev. Cell 4, 307-319.
Pawley, J. B. (1995). "Handbook of Biological Confocal Microscopy," 2nd Ed. Plenum Press, New York.
Pawley, J. B. (2000). The 39 steps: A cautionary tale of quantitative 3-D fluorescence microscopy. BioTechniques 28, 884-888.
Periasamy, A., Shoglund, P., Noakes, C., and Keller, R. (1999). An evaluation of two-photon versus confocal and digital deconvolution fluorescence microscopy imaging in Xenopus morphogenesis. Microsc. Res. Techn. 47, 172-181.
Scalettar, B. A., Swedlow, J. R., Sedat, J. W., and Agard, D. A. (1996). Dispersion, aberration and deconvolution in multi-wavelength fluorescence images. J. Microsc. 182(1), 50-60.
Sheppard, C. J. R., Gan, X., Gu, M., and Roy, M. (1995). Signal-tonoise in confocal microscopes. In "The Handbook of Biological Confocal Microscopy" (J. B. Pawley, ed.), 2nd Ed., pp. 363-371. Plenum Press, New York.
Swedlow, J. R., Hu, K., Andrews, P. D., Roos, D. S., and Murray, J. M. (2002). Measuring tubulin content in Toxoplasma gondii: A comparison of laser-scanning confocal and wide-field fluorescence microscopy. Proc. Natl. Acad. Sci. USA 99, 2014- 2019.
Van der Voort, H. T. M. (1997). Image restoration in one- and two- photon microscopy. Online at URL: http://www.svi.nl/ education/#Discussions (accessed July 5th 2004).
VanKempen, G. M. P., vanVliet, L. J., Verveer, P. J., and vanderVoort, H. T. M. (1997). A quantitative comparison of image restoration methods for confocal microscopy. J. Microsc. 185(3), 354-365.
Wallace, W., Schaefer, L. H., and Swedlow, J. R. (2001). A working person's guide to deconvolution in light microscopy. BioTechniques 31, 1076-1097.
Wiegand, U. K., Duncan, R. R., Greaves, J., Chow, R. H., Shipston, M. J., and Apps, D. K. (2003). Red, yellow, green go! A novel tool for microscopic segregation of secretory vesicle pools according to their age. Biochem. Soc. Trans. 31, 851-856.