Isolation of individual spores of a linear tetrad and keeping a record of the linear order of analysed spores is a laborious process. Therefore, sometimes by choice even ordered tetrads are analysed without any record of their linear order. For this purpose, in a fungus like
Neurospora, the spores are shot out of ascus and may be caught (on a collection surface) scattered without retaining their linear order. In other cases, like
Chlamydomonas, Ascobolus or yeast, the ordered tetrads are not available and therefore analysis of unordered tetrads is conducted not by choice but by compulsion. In either case, the analysis- of unordered tetrads is simpler, though less informative.
The unordered tetrads, like the ordered tetrads discussed earlier, can be classified into PD, NPD and T, although individual tetrads can not be classified as products of
first division segregation and
second division segregation. In view of this, although linkage between any two genes can be detected, centromere mapping will not be possible.
As discussed earlier for ordered tetrads, the critical test for linkage is the absence of equality between PD and NPD and excess of T relative to NPD. This can be tested by a statistical test (e.g. χ
2test). This feature is illustrated in Figures. 11.12 and 11.13, where relationships of the relative frequencies of PD, NPD and T are shown for unlinked and linked loci.
It can be shown that the maximum frequency of M
II segregation for a gene is 66.7%. When two loci are considered, M
II segregation for one locus in combination with M
I segregation for the second locus gives a maximum frequency of 66.7% for tetratype (T) tetrads. The minimum frequency for either PD or NPD is 16.7. These frequencies hold good for independent assortment. But for linked loci, with increase in the intensity of linkage, frequency of PD increases and the frequencies of NPD and T go down, the frequency of T always remaining higher than NPD. These relationships can be theoretically proved (Suzuki
et al., 1989).
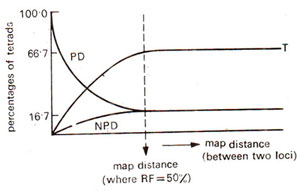
Fig. 11.12. Frequencies of different types of tetrads for linked loci (redrawn from Suzuki et al., 1986).
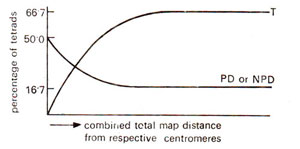
Fig. 11.13. Frequencies of different types of tetrads for unlinked loci (redrawn from Suzuki et al., 1986).
As suggested above, if PD = NPD, then RF = 50% indicating independent assortment, but we can not say whether the genes are on different chromosomes or are located distantly apart on same chromosome. In such a situation T type tetrads can be of some use. In an example, where PD = 42, NPD = 48 and T = 10, the tetratype frequency of T = 10 is incompatible with our graph representing linked loci, where T is always more than NPD, and for RF = 50%, T = 66.7%. Therefore, the data suggest that the loci concerned are on separate chromosomes.
It should also be recognized that a maximum frequency of 66.7% for M
II gives RF = 33.3% and not the expected 50%. This is due to multiple crossovers. In tetrads, a method is available to correct trapping errors due to double crossovers.
If
we assume a region having no more than two crossovers or double crossovers (DCO), the NPD resulting from four strand double crossovers, will be 1/4 of DCO (Fig. 10.14 in
Linkage and Crossing Over in Diploid Organisms (Higher Eukaryotes)), so that DCO = 4 NPD. Similarly tetratypes (T) result from single crossovers (SCO) + 50% of DCO (three strand DCO) so that SCO can be calculated from T and NPD as follows : SCO = T - 50% DCO = T - 2NPD. The crossover value 'm' will be = SCO + 2(DCO) = (T - 2NPD) + 2(4NPD) = T + 6NPD. This value represents the number of crossovers and needs to be halved to get RF value, so that

This formula has an advantage over the mapping function described in
Linkage and Crossing Over in Diploid Organisms (Higher Eukaryotes), since it does not assume lack of chiasma interference, while mapping function does assume lack of interference. However, this approach, like mapping function, corrects the errors in mapping due to multiple crossovers.
Similarly, tetrad analysis can be conducted when three gene differences are involved (for details, consult Strickberger's
Genetics).
Mitotic Recombination and Chromosome Mapping
Mitotic recombination is a phenomenon, which though, first detected in
Drosophila, has been extensively utilized in
Aspergillus (a fungus) for detection and measurement of linkage. Therefore, before discussing its nature and utility in
Aspergillus, the phenomenon of mitotic crossing over, as first discovered in
Drosophila, will be described in brief.
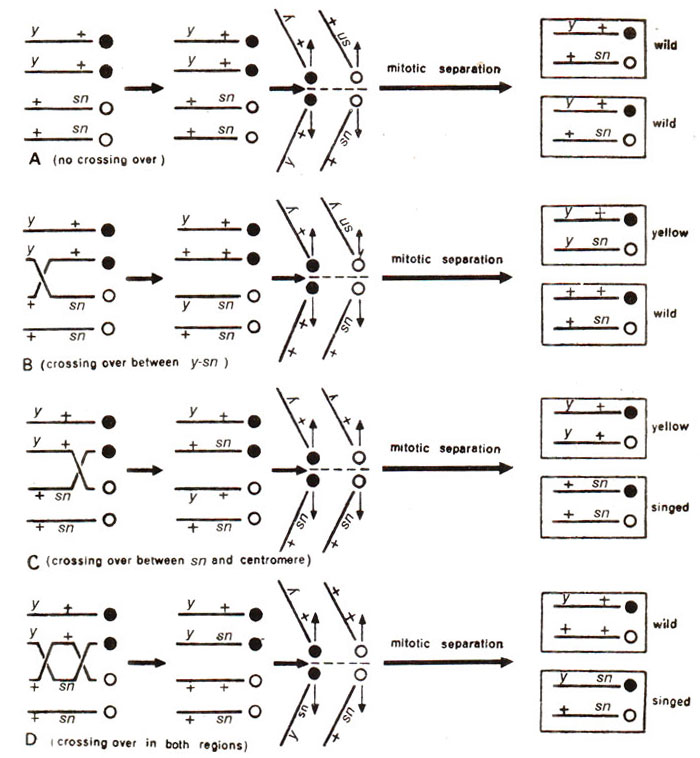
Fig. 11.14. Explanation of results due to normal mitosis and mitotic crossing over in different regions of two X chromosomes of a female Drosophila fly, heterozygous for yellow colour (y) and singed bristles (sn) (modified from Strickberger's "Genetics").
Somatic crossing over in
Drosophila In 1936,
Stern studied somatic crossing over between morphological mutants
yellow body colour and
singed bristles (bent blunted bristles). Somatic crossing over was inferred from presence of
twin spots found in adjacent regions. Crossing over in such somatic tissues has also been found to be enhanced due to presence of genes such as
'minute'. Let us now consider crossing over in a fly which is heterozygous for both these genes found in 'trans' configuration or 'repulsion phase' (y +/+
sn). Since it is heterozygous for both the genes which are recessive, only wild phenotype will normally appear (Fig. 11.14 A) except due to somatic crossing over. If the order of genes is
y-
sn-centromere, then following three possibilities of crossing over exist.
Crossing over between y-sn. As can be seen in Figure 11.14 B, crossing over between
y-sn leads to production of two cells with
y+/ysn (yellow) and + +/+
sn (wild) genotypes, so that a single yellow spot will appear wherever crossing over between
y-sn region occurs.
Crossing over
between sn-centromere. Crossing over between sn-centromere region leads to twin spots, yellow and singed with genotypes
y+/y+ and
+sn/+sn (Fig. 11.14 C).
Double crossing over
(y-sn and sn-centromere regions). Double crossing over results in single spots with singed bristles (y
sn/+sn), the other product of crossing over giving wild phenotype, i.e. y+/+ + (Fig. 11.14 D).

Fig. 11.14. Explanation of results due to normal mitosis and mitotic crossing over in different regions of two X chromosomes of a female Drosophila fly, heterozygous for yellow colour (y) and singed bristles (sn) (modified from Strickberger's "Genetics").
It was observed by Stern in his study that yellow and singed twin spots were most frequent. This was in agreement with earlier data from meiotic recombination, where it could be shown that the distance between
sn-centromere is longest and that between
y and
sn is relatively very small.









