Lambertian Surfaces
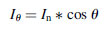 (5.22)
(5.22)Therefore, even if the luminous intensity decreases with a factor cos(θ) from the normal, the projected surface decreases with the same factor; as a consequence, the radiance (luminance) of a Lambertian surface is the same regardless of the viewing angle and is given by:
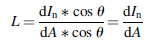 (5.23)
(5.23)It is worthwhile to note that in a Lambertian surface the ratio between the radiant exitance and the radiance is π and not 2π:
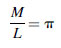 (5.24)
(5.24)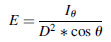 (5.25)
(5.25)and from Lambert’s cosine law [Equation (5.22)], we have:
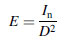 (5.26)
(5.26)which simply says that the irradiance (radiant flux density) of any point P on the inside surface of S is a constant.
This is interesting. From the definition of irradiance [Equation (5.9)], we know that Φ = E * A for constant flux density across a finite surface area A. As the area A of the surface of a sphere with radius r is given by:
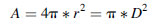 (5.27)
(5.27)we have:
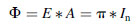 (5.28)
(5.28)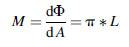 (5.29)
(5.29)This explains, clearly and without resorting to integral calculus, where the factor of p comes from.




