Units Conversion
- 1 J (joule) = 1 W sec (watt * second)
- 1 W (watt) = 683.0 lm (photopic) at 555 nm = 1700.0 lm (scotopic) at 507 nm
- 1 lm = 1.464 x 10-3 W at 555 nm = 1/(4π) candela (cd) (only if isotropic)
- 1 lm sec-1 (lumen seconds-1) = 1.464 x 10-3 J at 555 nm.
A monochromatic point source with a wavelength of 510 nm with a radiant intensity of 1/683 W sr-1 has a luminous intensity of 0.503 cd, as the photopic luminous efficiency at 510 nm is 0.503.
A 680 nm laser pointer with the power of 5 mW produces 0.005 W 0.017 683 lm W-1 = 0.058 lm, while a 630 nm laser pointer with a power of 5 mW produces 0.905 lm, a significantly greater power output.
Some sources are easier to do this with than others. A standard incandescent lamp produces a continuous spectrum in the visible, and various intervals must be used to determine the luminous flux. For sources like a mercury vapor lamp, however, it is slightly easier. Mercury emits light primarily in a line spectrum. It emits radiant flux at six primary wavelengths. This makes it easier to determine the luminous flux of this lamp versus the incandescent.
Irradiance (Flux Density)
- 1 W m-2 = 10-4 W cm-2 = 6.83 x 102 lux (lx) at 555 nm
- 1 lmm-2 = 1 lx = 10-4 lm cm-2
- 1 photon at 400 nm = 4.96 x 10-19 J
- 1 W m-2 at 400 nm = 1 J m-2 sec-1 = 3.3 µmol m-2 s21 = 3.3 µEinsten m-2 sec-1
- 1 photon at 500 nm = 3.97 x 10-19 J
- 1 W m-2 at 500 nm = 1 J m-2 sec-1 = 4.2 µmol m-2 sec-1 = 4.2 µEinsten m-2 sec-1
- 1 photon at 600 nm = 3.31 x 10-19 J
- 1 W m-2 at 600 nm = 1 J m-2 sec-1 = 5.0 µmol m-2 sec-1 = 5.0 µEinsten m-2 sec-1
- 1 photon at 700 nm = 2.83 x 10-19 J
- 1 W m-2 at 700 nm = 1 J m-2 sec-1 = 5.9 µmol m-2 sec-1 = 5.9 µEinsten m-2 sec-1
Radiance
- 1 W m-2 sr-1 = 6.83 x 102 lm m-2 sr-1 at 555 nm = 683 cd cm-2 at 555 nm
Radiant Intensity
- 1 W sr-1 = 12.566 W (isotropic) = 4π W = 683 cd at 555 nm
Luminous Intensity
- 1 lm sr = 1 cd = 4π lm (isotropic) = 1.464 x 10-3 W sr-1 at 555 nm
Luminance
- 1 lmm-2 sr-1 = 1 cd m-2 = 10-4 lm cm-2 sr-1 = 10-4 cd cm-2
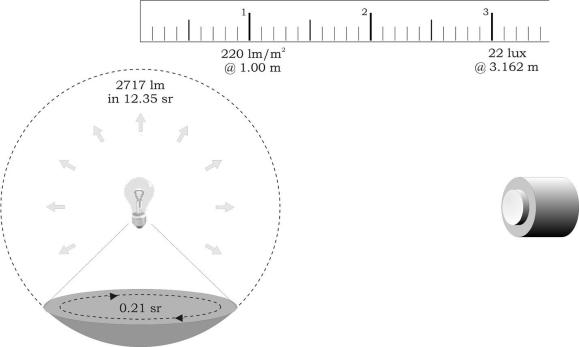
Converting between geometry-based measurement units is difficult, and should only be attempted when it is impossible to measure in the actual desired units. You must be aware of what each of the measurement geometries implicitly assumes before you can convert. The example below shows the conversion between lux and lumens.
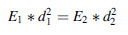 (5.15)
(5.15)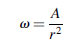 (5.4)
(5.4)If you measure 22.0 lux from a light bulb at a distance of 3.162 m, how much light, in lumens, is the bulb producing? Assume that the lamp is an isotropic point source, with the exception that the base blocks a 30° solid angle. Using Equation (5.15), the irradiance at 1.0 m is E1.0 m = (3.162/1.0)2 x 22.0 = 220 lm m-2. On the basis of steradian definition [Equation (5.4)], we know that 1 sr cuts off a spherical surface area of 1 m2 at a distance of 1 m from the source. Therefore, 220 lm m-2 corresponds to 220 lm sr-1 . The solid angle of the lamp is equal to 2π hr-1 [Equation (5.4)], where h is the height of the spherical calotte, and corresponds to 2π x [1–cos (360 230/ 2)] = 12.35 sr, while the shadowed solid angle corresponds to 0.21 sr. Therefore, the total lumen output will be 220 lm x sr-1 12.35 sr = 2717 lm, (Figure 5.13).