Multifactorial experiments

The simplest experiments are those in which one treatment (factor) is applied at a time to the samples. This approach is likely to give clear-cut answers, but it could be criticized for lacking realism. In particular, it cannot take account of interactions among two or more conditions that are likely to occur in real life. A multifactorial experiment (Fig. lOA) is an attempt to do this; the interactions among treatments can be analysed by specialized forms of analysis of variance.

Multifactorial experiments are economical on resources because of 'hidden replication'. This arises when two or more treatments are given to a subject because the result acts statistically as a replicate for each treatment. Choice of relevant treatments to combine is important in multifactorial experiments; for instance, an interaction may be present at certain concentrations of a chemical but not at others (perhaps because the response is saturated). It is also important that the measurement scale for the response is consistent, otherwise spurious interactions may occur. Beware when planning a multifactorial experiment that the numbers of replicates do not get out of hand: you may have to restrict the treatments to 'plus' or 'minus' the factor of interest (as in Fig. 10.4).

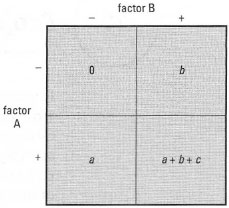Fig. 10.4 Design of a simple multifactorial experiment. Factors A and B have effects a and b when applied alone. When both are applied together, the effect is denoted by a + b + c.

*Diagram:

1. If c = 0, there is no interaction (e.g. 2 + 2 + c = 4).
2. If c is positive, there is a positive interaction (synergism) between A and B (e.g. 2 + 2 + c = 5).
3. If c is negative, there is a negative interaction (antagonism) between A and B (e.g. 2 + 2 + c = 3).