In the beginning of the present century, after rediscovery of Mendel's laws, segregation ratios of 3:1 in F
2 generation and 1 : 1 in test crosses were demonstrated to hold good in a variety of plants and animals. However, later,
Yule and others argued that dominant and recessive alleles would reach a stable equilibrium frequency of 3 : 1 in a population irrespective of their initial frequencies. Such a hypothesis was later proved to be wrong and alterations in gene frequencies were noted. In 1908,
G.H. Hardy, an English mathematician and
W. Weinberg, a German physician independently discovered that an equilibrium is established between frequencies of alleles in a random mating population. It was also shown that the relative gene frequencies remained unaltered from one generation to the next, regardless of their dominance and recessive relationship. A mathematical relationship called
Hardy- Weinberg Theorem was developed to explain this equilibrium. This is now known as
Hardy- Weinberg Law.
Frequencies of two alleles at a single locus
We already know that when two individuals heterozygous for the same gene e.g.
Aa are crossed (
Aa x
Aa)
, they segregate in a ratio 1
AA : 2
Aa : 1
aa. This ratio can be obtained by simple expansion of binomial (
A + a)
2 = 1
AA + 2
Aa + \aa. In this case, frequencies of
A and
a are the same i.e. 0.5. However, in a population the frequencies of two alleles belonging to a particular gene are not always the same and therefore, in a random mating population the above ratio of 1 : 2 : 1 is not always available. Suppose
'p' represents the frequency of allele
'A' and
'q' represents the frequency of V (where
p + q = 1), then these frequencies
'p' and
'q' can also be realised in the form of gametes carrying
'A' and
'a'.
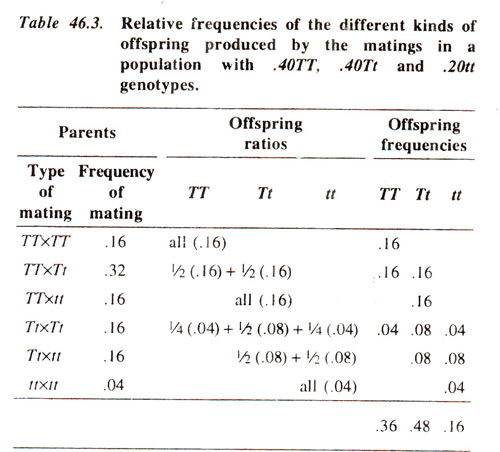
In other words, the proportion of gametes carrying
'A' will be
'p' and the proportion of gametes carrying
'a' will be
'q'. The probabilities of individuals obtained from random mating from such a population can be obtained as shown in Figure 46.1. It can be seen in the figure that the probability of homozygous dominant (
AA)obtained through random mating would be
'p2', that of heterozygous (
Aa)individuals would be
'2pq' and that of homozygous recessive (
aa)would be '
q2'. This leads to the formulation of
Hardy-Weinberg Equation :
p2 (AA)' + 2pq (Aa) + q2 (aa).
Fig. 46.1. The results, showing frequencies of three genotypes produced due to random mating in a population having allele 'A' with a frequency 'p' and allele 'a' with frequency 'q'.
This equation would be obtained in every case after
one generation of random mating, if factors like mutation, selection and migration do not operate. In a particular heterogeneous population where for a particular character complete dominance is expressed, no distinction can be made between homozygous dominant (AA) and heterozygous (
Aa)individuals. Therefore,
it would not be possible to determine the value of
'p' directly but indirectly as '1 -
q',by first determining the value of '
q' Individuals exhibiting recessive characters will be only homozygous for recessive allele (
aa)and their frequency at equilibrium state would be
'q2', so that the value of
'q' can be obtained through simple square root of frequency of the individuals having recessive phenotype. Since
p + q = 1,
p will be equal to '1 -
q'Substituting the value '1 -
q' for
'p' in the
Hardy Weinberg Equation, we can get modified form of this equation which can be written as (1 -
q)
2 + Iq (1 -
q)
+ q2 = 1.

Fig. 46.1. The results, showing frequencies of three genotypes produced due to random mating in a population having allele 'A' with a frequency 'p' and allele 'a' with frequency 'q'.
It is possible to prove algebraically that a population having genotypic frequencies expressed as
p2 + 2pq + q2 will be in equilibrium. In doing so, as shown in Table 46.1, there are six possible types of matings using three genotypes. Taking the example of alleles
'A' and
'a', the possible matings will be
AA x
AA, AA x
Aa, AA x
aa, Aa x
Aa, Aa x
aa and
aa x
aa. Out of these six possible matings. whenever genotypes of the two parents differ, the mating can take place in two different ways using either of the genotypes as female parent. Since frequencies of different parental genotypes are known from the equilibrium equation, frequencies of progeny can be obtained as depicted in Table 46.2. It will be seen from the table that the progeny will still exhibit the same proportions between three genotypes as shown in
Hardy-Weinberg Equation i.e.
p2 + 2pq + q2.
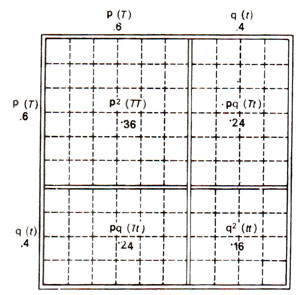
Fig. 46.2. Frequencies of genotypes generated under conditions of random mating for two alleles - T (taster) and t (nontaster) at a locus, when their respective frequencies are p = 0.6 and q = 0.4 (redrawn from Strickberger's 'Genetics').
A particular population may not be in equilibrium at a particular time. In such a case, distribution of alleles in succeeding generations, resulting due to random mating, can be calculated by using Hardy-Weinberg Equation :
p2 +
2pq + q2. For instance, one may try to find out frequencies of alleles of a gene controlling tasting ability among human beings for the chemical
phenylthiocarbamide (PTC). PTC is a chemical with bitter taste, which can be experienced only by certain fraction of human beings. This character of tasting ability and the difference between those who can taste and those who can not taste
PTC, resides in a single gene difference with two alleies '
T' and
't'. Since T' is dominant over
't',the tasters can have two genotypes (
TT and
Tt)
, whereas the non-tasters will have only one genotype (
tt)
. Suppose in an initial population of human beings,
different genotypes are represented by ratio .40
TT : .40
Tt : .20
tt. The gene frequencies, obviously, will be
T = .40 (
TT)+ ½x .40 (
Tt)
= .60;
t = .20 (
tt)
+ ½x .40 (
Tt)
= .40. The frequencies of
T = .60 and
t = .40 will give a genotypic ratio of .36
TT : .48
Tt : .16
tt in the next generation. This has been explained in detail in Table 46.3, and illustrated in Figure 46.2, where frequencies of different mating types and frequencies of different genotypes in the progeny from each mating type are given. This ratio will be available only when marriages within the population are arranged regardless of tasting ability or, in other words, we can say that the marriages are at random regarding the tasting ability.

Fig. 46.2. Frequencies of genotypes generated under conditions of random mating for two alleles - T (taster) and t (nontaster) at a locus, when their respective frequencies are p = 0.6 and q = 0.4 (redrawn from Strickberger's 'Genetics').
One can see from this ratio that although the genotype frequencies have changed, but gene frequencies did not change. This can be illustrated by calculating the gene frequencies from the above genotypic ratio. In this case '
T'will be equal to .36 (
TT)
+ ½ x .48 (
Tt)= .60 and
't' will be equal to .16 (
tt)
+ ½ x .48 (
Tt)
= 0.40. However, it can be shown that genotypic ratio 0.36
TT + .48
Tt + .16
tt will give the same genotypic ratio in the following generation. This demonstrates that after one generation of random mating, equilibrium in the genotypic ratio can be achieved and this will follow the Hardy-Weinberg Equation.
In view of the above, following conclusions can be made : (i) In a large
panmictic population, where different genotypes are equally viable, gene frequencies of a particular generation will be similar to and depend upon gene frequencies of previous generations and not upon its genotype frequencies, (ii) The frequencies of different genotypes produced due to random mating will depend upon the gene frequencies and will reach an equilibrium after one. single generation of random mating.