In the above example, we have considered a situation where only two alleles at a single locus are present. The situation will become slightly complicated when genes with three or more alleles are taken into consideration. An analysis of gene frequencies and genotype frequencies involving situations having more than two alleles at a locus can be undertaken from any one of the following three approaches :
(1) If frequencies of genotypes are determined with references to only one allele
'A1' (
A1is one of the several alleles, namely
At, A2, A
3, ...,
An)
, then we can presume that the frequency of this particular allele in population
:s
'p' and the sum total of frequencies of all other alleles is
q (where
p+q = 1). In such a situation, at the equilibrium stage the genotypic frequencies can be represented as :
p2(
A1A1)
+ 2
pq (
A1A2 +
A1A3… +
A1An) +
q2 (
A2A2 +
A3A3… +
AnAn).
In such a situation we are ignoring all heterozygotes which do not involve the particular allele in question i.e.,
'A1'. For instance
A2A3,
A2A4or
A3A4are not included. Consequently, in this case although
p +
q = 1, but the total frequency of all the genotypes included in the equilibrium equation will not be equal to one (some genotypes are excluded).
(2) We may also determine genotype frequencies involving only two of the several alleles in a multiple allelic series. As an example we may take '
A1' and
' A2' as two such alleles and their corresponding gene frequencies as
q1and
q2 respectively so that
q1 + q2 ≠ 1, because frequencies of several other alleles are not included. The genotypic frequencies involving the two alleles at the equilibrium stage can be written in the form of Hardy Weinberg Equilibrium Equation as :
q12 A1A1 +
2q1q2A1A2 + q22A2A2. In this case, neither the total gene frequency of '
A1' and '
A2' will be unity nor will the frequencies of genotypes involving the two alleles be unity.
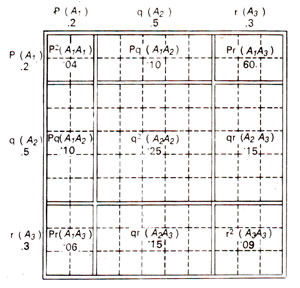
Fig. 46.3. Frequencies of genotypes generated under conditions of random mating when there are three alleles A1, A2, A3present at a locus, and their gene frequencies are p = 0.2, q = 0.5 and r = 0.3
(3) In the above two conditions, the multiple allelic-series was reduced to a two allele series for purpose of simplification. However, it is possible to determine frequencies of genotypes involving three or more alleles at the equilibrium stage. In this case, each allelic frequency will have to be considered as an element in a multinomial expansion. For instance, if there are three alleles '
A1', '
A2' and '
A3' at the locus, with their corresponding gene frequencies
'p', 'q' and
'r' respectively, then
p+q+r = 1. In such a case the trinomial expansion i.e. (
p+q+r)
2 =
p2 A1A1 + 2
pq A1A2 + 2
pr A1A3 + q2 A2A2 + 2
qr A2A3 + r2 A3A3 will represent the genotypic frequencies at the equilibrium stage.
It can be realized that in this case zygotic combinations between haploid gametes will depend upon frequencies of individual alleles because each haploid gamete contains a single allele at a particular locus as shown in Figure 46.3. Equilibrium will be established in this case also within a single generation of random mating.

Fig. 46.3. Frequencies of genotypes generated under conditions of random mating when there are three alleles A1, A2, A3present at a locus, and their gene frequencies are p = 0.2, q = 0.5 and r = 0.3





