Migration
Mutations introduce new genes into a population, however, it is not the only mechanism to do so. Through 'migration' also, recessive alleles can be introduced into a population from a nearby population. In such a case, the difference in frequencies between the two populations and the proportion of migrant genes that are incorporated in each generation are two most important factors in determining Δq. Let 'm' be the proportion of immigrants in each generation and ' 1 - m' be the natives, in a large population. Let the frequency of a particular gene be 'qm' and 'q0' among immigrants and natives respectively, then the frequency of the gene in the mixed population i.e. q1will be :
It means, in one generation, the expression Δq takes the form :
Δq = m (qm - q0)
After 'n' generations, the frequency of the gene becomes qn and then we have :
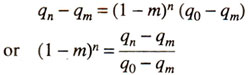
As this equation depends upon five factors. viz., qn, q0, qm, m and n, knowledge of any four will lead to determination of fifth factor.
Random drift
As earlier discussed, while the factors, mutation, selection and migration, are directional in influencing the gene frequencies, random drift is a non-directional factor. In this connection when we consider an actual situation, we have to realize that we always take into account only a sample of a population. This sample of a population, although representative of the population, may not have exactly the same gene frequency as found in the population. Such deviations in gene frequencies will be due to sampling errors. The extent of this sampling error will also depend upon the size of sample.
For instance, if only a few parents are chosen to begin a new population, the gene frequency of this new population may deviate widely from the gene frequencies of the original population, because in this case' the sampling error will be high. On the other hand, if the sample size is large, i.e., if a large number of parents are taken to begin a new population, deviation in the gene frequencies may not be so large. In either case, however, the deviation in the gene frequency can be measured with the help of standard deviation σ = √pq/N, where p and q are the original frequencies of the alleles and N is the number of genes sampled. The number of genes (population size) sampled will be equal to double the number of parents or individuals sampled from original population in case of a diploid parent, because in a diploid there would be two homologous chromosomes of each type, each carrying one gene at a particular locus. Therefore, the above formula σ= √pq/N will take the form σ= √pq/2N, where N is the number of actual parents. The readers should remember that while in the former formula (σ = √pq/N), N is the number of genes sampled, in the latter formula (σ = √pq/2N), N is the number of parents.
To illustrate the above let us take an example when p = q = 0.5 and the population is continued using 1000 individuals. Then using the formula σ = √pq/N, σwill be equal to √(0.5 x 0.5)/2000 = √0.25/2000 = 0.011. this would mean that the values of gene frequency of the new population will fluctuate around 0.5 ± 0.011, which means that 68% of the population derived in this manner will have gene frequencies of the two alleles ranging between 0.511 to 0.489. Contrary to this, if we consider a hypothetical case where a new population is initiated by taking two individuals then σ= √(0.5 x 0.5)/4 = √0.0625, which means that the values will fluctuate around 0.5 ± 0.25 i.e. -0.25 to 0.75. In actual practice, therefore, the gene frequencies due to random drift may approach the two limits that is 0 and 1. This would be possible only when new population arises due to a very small sample leading to the fixation of one allele at the cost of the other. In this manner, the changes in the gene frequencies can be brought about without the existence of any directional force i.e. mutation, selection and migration, and this change in gene frequency has been called random genetic drift.
After 'n' generations, the frequency of the gene becomes qn and then we have :
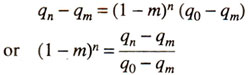
As this equation depends upon five factors. viz., qn, q0, qm, m and n, knowledge of any four will lead to determination of fifth factor.
As earlier discussed, while the factors, mutation, selection and migration, are directional in influencing the gene frequencies, random drift is a non-directional factor. In this connection when we consider an actual situation, we have to realize that we always take into account only a sample of a population. This sample of a population, although representative of the population, may not have exactly the same gene frequency as found in the population. Such deviations in gene frequencies will be due to sampling errors. The extent of this sampling error will also depend upon the size of sample.




