Mendel’s Second Law
Mendel’s Second Law
According to Mendel’s law of independent
assortment, genes located
on different pairs of homologous chromosomes
assort independently during
meiosis. Thus the law deals with genes
for two different characters that are
borne on two different pairs of chromosomes.
Mendel carried out experiments
on peas that differed from each
other at two or more genes, that is,
experiments involving two or more
phenotypic characters.
Mendel had already established that tall plants were dominant to dwarf. He also noted that crosses between plants bearing yellow seeds and plants bearing green seeds produced plants with yellow seeds in the F1 generation; therefore yellow was dominant to green.
The next step was
to make a cross between plants differing
in these two characteristics.
When
a tall plant with yellow seeds (T/T Y/Y)
was crossed with a
dwarf plant with
green seeds (t/t
y/y), the F1 plants
were tall and yellow
as expected
(T/t Y/y).
The F1 hybrids
were then crossed
with each other, and the F2 results are
shown in Figure 5-6.
Mendel already knew that a cross between two plants bearing a single pair of alleles of the genotype T/t would yield a 3:1 ratio. Similarly, a cross between two plants with the genotypes Y/y would yield the same 3:1 ratio. If we examine only the tall and dwarf phenotypes expected in the outcome of the dihybrid experiment, they produce a ratio of 12 tall to 4 dwarf, which reduces to a ratio of 3:1. Likewise, a total of 12 plants have yellow seeds for every 4 plants that have green—again a 3:1 ratio. Thus the monohybrid ratio prevails for both traits when they are considered independently. The 9:3:3:1 ratio is nothing more than a combination of the two 3:1 ratios.
When one of the alleles is unknown, it can be designated by a dash (T/—). This designation can also be used when it is immaterial whether the genotype is heterozygous or homozygous, as when we total all of a certain phenotype.The dash could be either T or t.
The F2 genotypes and phenotypes are as follows:
The results of this experiment show that the segregation of alleles for plant height is entirely independent of the segregation of alleles for seed color. Neither has any influence on the other. Thus another way to state Mendel’s law of independent assortment is that allelic variants of different genes on different chromosomes segregate independently of one another. The reason is that during meiosis the member of any pair of homologous chromosomes received by a gamete is independent of which member of any other pair of chromosomes it receives. Of course, if the genes were on the same chromosome, they would assort together (be linked) unless crossing over occurred.
One way to estimate proportions of progeny with a given genotype or phenotype is to construct a Punnett square. With a monohybrid cross, this is easy; with a dihybrid cross, a Punnett square is rather laborious; and with a trihybrid cross, it is very tedious. We can make such estimates much more easily by taking advantage of simple probability calculations. The basic assumption is that all the genotypes of gametes of one sex have an equal chance of uniting with all the genotypes of gametes of the other sex, in proportion to the numbers of each present. This is generally true when the sample size is large enough, and the actual numbers observed come close to those predicted by the laws of probability.
We may define probability as follows:

For example, the probability (p) of a coin falling heads when tossed is ½, because the coin has two sides. The probability of rolling a three on a die is 1/6, because the die has six sides.
The probability of independent
events occurring together (ordered
events) involves the product rule,
which is simply the product of their
individual probabilities.
When two
coins are tossed together, the probability
of getting two heads is ½ × ½ =
¼, or 1 chance in 4. The probability
of rolling two threes simultaneously
with two dice is as follows:
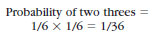
Note, however, that a small sample size may give a result quite different from that predicted. Thus if we tossed the coin three times and it fell heads each time, we would not be much surprised. But if we tossed the coin 1000 times, and the number of times it fell heads diverged very much from 500, we would strongly suspect that there was something wrong with the coin.
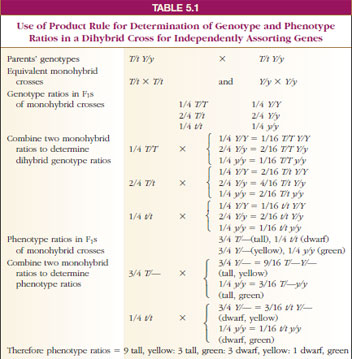
We can use the product rule to predict the ratios of inheritance in monohybrid or dihybrid (or larger) crosses if the genes sort independently in the gametes (as they did in all of Mendel’s experiments) (Table 5-1).
Multiple Alleles
Earlier we defined alleles as the alternate forms of a gene. Whereas an individual can have no more than two alleles at a given locus (one each on each chromosome of the homologous pair),
many more dissimilar alleles
can exist in the population. An
example is the set of multiple alleles
that affects coat color in rabbits. The different
alleles are C (normal color), ccb (chinchilla color), cb (Himalayan color),
and c (albino). The four alleles fall into
a dominance series with C dominant
over everything. The dominant allele is
always written to the left and the recessive
to the right:
Multiple alleles arise through mutations at the same gene locus over periods of time. Any gene may mutate if given time and thus can give rise to slightly different alleles at the same locus.
Gene Interaction
The types of crosses previously described are simple in that the character variation involved results from the action of a single gene, but many cases are known in which the variation of a character is the result of two or more genes. Mendel probably did not appreciate the real significance of the genotype, as contrasted with the visible character—the phenotype. We now know that many different genotypes may affect a single phenotype (polygenic inheritance).
Also, many genes have more than a single effect on organismal phenotypes, a phenomenon called pleiotropy. A gene for eye color, for instance, may be the ultimate cause of eye color, yet at the same time it may be responsible for influencing the development of other characters as well. An allele at one locus may mask or prevent the expression of an allele at another locus acting on the same trait, a phenomenon called epistasis. Another case of gene interaction is that in which several sets of alleles may produce a cumulative effect on the same character.
Several characters in humans are polygenic. In such cases the characters, instead of having discrete alternative phenotypes, show continuous variation between two extremes. This is sometimes called blending, or quantitative inheritance. In this kind of inheritance the children are often more or less intermediate between the two parents.
One illustration of such a type is the degree of pigmentation in matings between the black and white human races. The cumulative genes in such matings have a quantitative expression. Three or four genes are probably involved in skin pigmentation, but we will simplify our explanation by assuming that there are only two pairs of independently assorting genes. Thus a person with very dark pigment has two genes for pigmentation on separate chromosomes (A/A B/B). Each dominant allele contributes one unit of pigment. A person with very light pigment has alleles (a/a b/b) that contribute no color. (Freckles that commonly appear in the skin of very light people represent pigment contributed by entirely separate genes.) The offspring of very dark and very light parents would have an intermediate skin color (A/a B/b).
The inheritance of eye color in humans is another example of gene interaction.One allele (B) determines whether pigment is present in the front layer of the iris.This allele is dominant over the allele for the absence of pigment (b).The genotypes B/B and B/b pigment generally produce brown eyes, and b/b produces blue eyes.However, these phenotypes are greatly affected by many modifier genes influencing, for example, the amount of pigment present, the tone of the pigment, and its distribution. Thus a person with B/b may even have blue eyes if modifier genes determine a lack of pigment, thus explaining the rare instances of a brown-eyed child of blueeyed parents.
The children of parents having intermediate skin color show a range of skin color, depending on the number of genes for pigmentation that they inherit. Their skin color ranges from very dark (A/A B/B), to dark (A/A B/b or A/a B/B), intermediate (A/A b/b or A/a B/b or a/a B/B), light (A/a b/b or a/a B/b), to very light (a/a b/b). It is thus possible for parents heterozygous for skin color to produce children with darker or lighter colors than themselves.
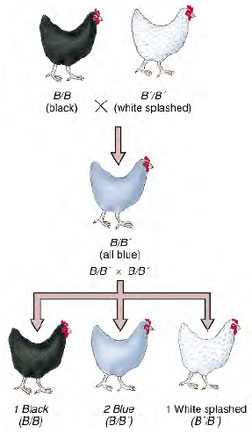 |
| Figure 5-5 Cross between chickens with black and splashed white feathers. Black and white are homozygous; Andalusian blue is heterozygous. |
Mendel had already established that tall plants were dominant to dwarf. He also noted that crosses between plants bearing yellow seeds and plants bearing green seeds produced plants with yellow seeds in the F1 generation; therefore yellow was dominant to green.
 |
Mendel already knew that a cross between two plants bearing a single pair of alleles of the genotype T/t would yield a 3:1 ratio. Similarly, a cross between two plants with the genotypes Y/y would yield the same 3:1 ratio. If we examine only the tall and dwarf phenotypes expected in the outcome of the dihybrid experiment, they produce a ratio of 12 tall to 4 dwarf, which reduces to a ratio of 3:1. Likewise, a total of 12 plants have yellow seeds for every 4 plants that have green—again a 3:1 ratio. Thus the monohybrid ratio prevails for both traits when they are considered independently. The 9:3:3:1 ratio is nothing more than a combination of the two 3:1 ratios.
| 3:1 × 3:1 = 9:3:3:1 |
When one of the alleles is unknown, it can be designated by a dash (T/—). This designation can also be used when it is immaterial whether the genotype is heterozygous or homozygous, as when we total all of a certain phenotype.The dash could be either T or t.
 |
The results of this experiment show that the segregation of alleles for plant height is entirely independent of the segregation of alleles for seed color. Neither has any influence on the other. Thus another way to state Mendel’s law of independent assortment is that allelic variants of different genes on different chromosomes segregate independently of one another. The reason is that during meiosis the member of any pair of homologous chromosomes received by a gamete is independent of which member of any other pair of chromosomes it receives. Of course, if the genes were on the same chromosome, they would assort together (be linked) unless crossing over occurred.
One way to estimate proportions of progeny with a given genotype or phenotype is to construct a Punnett square. With a monohybrid cross, this is easy; with a dihybrid cross, a Punnett square is rather laborious; and with a trihybrid cross, it is very tedious. We can make such estimates much more easily by taking advantage of simple probability calculations. The basic assumption is that all the genotypes of gametes of one sex have an equal chance of uniting with all the genotypes of gametes of the other sex, in proportion to the numbers of each present. This is generally true when the sample size is large enough, and the actual numbers observed come close to those predicted by the laws of probability.
We may define probability as follows:

For example, the probability (p) of a coin falling heads when tossed is ½, because the coin has two sides. The probability of rolling a three on a die is 1/6, because the die has six sides.
 |
Note, however, that a small sample size may give a result quite different from that predicted. Thus if we tossed the coin three times and it fell heads each time, we would not be much surprised. But if we tossed the coin 1000 times, and the number of times it fell heads diverged very much from 500, we would strongly suspect that there was something wrong with the coin.
We can use the product rule to predict the ratios of inheritance in monohybrid or dihybrid (or larger) crosses if the genes sort independently in the gametes (as they did in all of Mendel’s experiments) (Table 5-1).
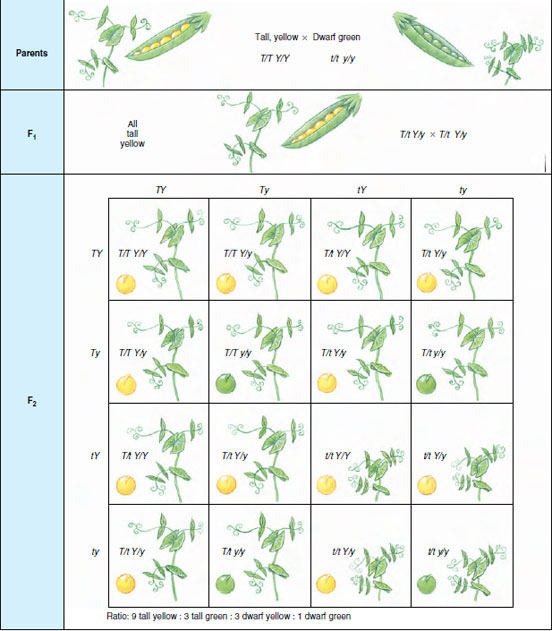 |
| Figure 5-6 Punnett square method for determination of genotypes and phenotypes expected in a dihybrid cross for independently assorting genes. |
Multiple Alleles
Earlier we defined alleles as the alternate forms of a gene. Whereas an individual can have no more than two alleles at a given locus (one each on each chromosome of the homologous pair),
 |
Multiple alleles arise through mutations at the same gene locus over periods of time. Any gene may mutate if given time and thus can give rise to slightly different alleles at the same locus.
Gene Interaction
The types of crosses previously described are simple in that the character variation involved results from the action of a single gene, but many cases are known in which the variation of a character is the result of two or more genes. Mendel probably did not appreciate the real significance of the genotype, as contrasted with the visible character—the phenotype. We now know that many different genotypes may affect a single phenotype (polygenic inheritance).
Also, many genes have more than a single effect on organismal phenotypes, a phenomenon called pleiotropy. A gene for eye color, for instance, may be the ultimate cause of eye color, yet at the same time it may be responsible for influencing the development of other characters as well. An allele at one locus may mask or prevent the expression of an allele at another locus acting on the same trait, a phenomenon called epistasis. Another case of gene interaction is that in which several sets of alleles may produce a cumulative effect on the same character.
Several characters in humans are polygenic. In such cases the characters, instead of having discrete alternative phenotypes, show continuous variation between two extremes. This is sometimes called blending, or quantitative inheritance. In this kind of inheritance the children are often more or less intermediate between the two parents.
One illustration of such a type is the degree of pigmentation in matings between the black and white human races. The cumulative genes in such matings have a quantitative expression. Three or four genes are probably involved in skin pigmentation, but we will simplify our explanation by assuming that there are only two pairs of independently assorting genes. Thus a person with very dark pigment has two genes for pigmentation on separate chromosomes (A/A B/B). Each dominant allele contributes one unit of pigment. A person with very light pigment has alleles (a/a b/b) that contribute no color. (Freckles that commonly appear in the skin of very light people represent pigment contributed by entirely separate genes.) The offspring of very dark and very light parents would have an intermediate skin color (A/a B/b).
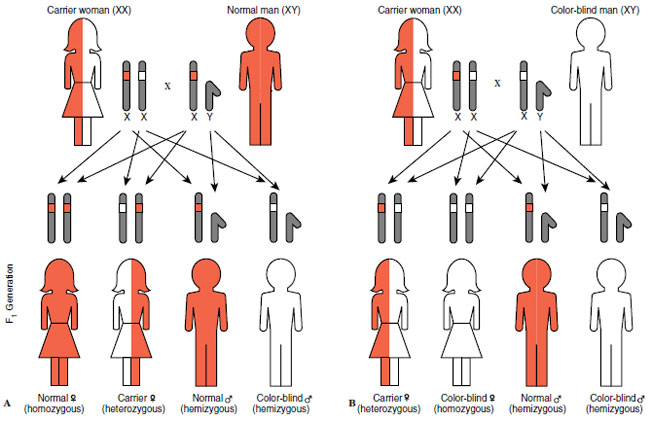 |
| Figure 5-7 Sex-linked inheritance of red-green color blindness in humans. A, Carrier mother and normal father produce color blindness in one-half of their sons but in none of their daughters. B, Half of both sons and daughters of carrier mother and color-blind father are color blind. |
The inheritance of eye color in humans is another example of gene interaction.One allele (B) determines whether pigment is present in the front layer of the iris.This allele is dominant over the allele for the absence of pigment (b).The genotypes B/B and B/b pigment generally produce brown eyes, and b/b produces blue eyes.However, these phenotypes are greatly affected by many modifier genes influencing, for example, the amount of pigment present, the tone of the pigment, and its distribution. Thus a person with B/b may even have blue eyes if modifier genes determine a lack of pigment, thus explaining the rare instances of a brown-eyed child of blueeyed parents.
The children of parents having intermediate skin color show a range of skin color, depending on the number of genes for pigmentation that they inherit. Their skin color ranges from very dark (A/A B/B), to dark (A/A B/b or A/a B/B), intermediate (A/A b/b or A/a B/b or a/a B/B), light (A/a b/b or a/a B/b), to very light (a/a b/b). It is thus possible for parents heterozygous for skin color to produce children with darker or lighter colors than themselves.




