Concentration
In SI units the concentration of a solute is expressed in mol m−3, which is essential for calculating specific parameters for substances, but which is inconvenient when dealing with solutions in the laboratory. A cubic metre (m−3) of water weighs approximately I ton! A common unit of volume used in chemistry is the litre (L): this is a non-SI unit and is converted to the SI unit of volume (m3) using 1.0 L = 10−3 m3. The concentration of a solute is usually symbolized by square brackets, e.g. [NaCI].A number of alternative ways of expressing the relative amounts of solute and solvent are in general use, and you may come across these terms in your practical work or in the literature.
Molarity
This is the term used to denote molar concentration, [C], expressed as moles of solute per litre volume of solution (mol L-1). This non-SI term continues to find widespread usage, in part because of the familiarity of working scientists with the term, but also because laboratory glassware is calibrated in millilitres and litres, making the preparation of molar and millimolar solutions relatively straightforward. However, the symbols in common use for molar (M) and millimolar (mM) solutions are at odds with the SI system and many people now prefer to use mol L-1 and mmol L-1 respectively, to avoid confusion. Details of some useful approaches to calculations involving molarities are given below:
- Preparing a solution of defined molarity. for a solute of known relative molecular (Mr), the following relationship can be applied:
[C] = mass of solute / Mr volume of solution
So, if you wanted to make up 200 ml (0.2L) of an aqeous solution of NaCl (Mr = 58.44g) at a concentration of 500 mmol L-1 (0.5 mol L-1), you could calculate the amount of Nacl required by inserting these values into eqn [6.1]:
0.5 = mass of solute / 58.44 0.2
which can be rearranged to
mass of solute = 0.5 × 0.2 × 58.44 = 5.844g
The same relationship can be used to calculate the soncentration of a solution containing a known amount of a solute, e.g. if 21.1g of NaCl wewe made up to a volume of 100 mL (0.1 L), this would give:
NaCl = 21.1/58.44 = 3.61 mol L-1 0.1
- Dilutions and concentrations. the following relationship is very useful if you are diluting (or concentrating) a solution:
[C1] V1 = [C2] V2
where [C1] and [C2] are the initial and final con-centrations, while V1 and V2 are their respective volumes: each pair must be expressed in the same units. Thus, if you wanted to dilute 200ml of 0.5mol L-1 NaCl to give a final molarity of 0.1 mol L-1, then, by substitution into eqn [6.2]:
0.5 × 200 = 0.1 × V2
Thus V2= 1000mL (in other words, you would have to add water to 200 mL of 0.5 mol L-1 NaCl to give a final volume of 1000 mL to obtain a 0.1 mol L-1 solution) - Interconversion: A simple way of interconversion amounts and volumes of any particular solution is to divide the amount and volume by a factor of 103.Thus a molar solution of a substance contains 1 mol L-1, which is equivalent to1 mmol mL-1or 1µmol µL-1,or 1 nmol nL-1 , etc. You may find this techinque useful when calculating the amount of substance present in a small wolume of solution of known concentration, e.g. to calculate the amount of NaCl present in 50µL of a solution with a concentration (molarity) of 0.5mol L-1 NaCl:
- thisis equivalent to 50 µmol µL-1
- therefore 50µl will contain 50 x 0.5 µmol = 25 µmol.
This is used to express the concentration of solute relative to the mass of solvent, i.e. mol kg-1. Molality is a temperature-independent means of expressing solute concentration, rarely used except when the osmotic properties of a solution are of interest.
Per cent composition (% wlw)
This is the solute mass (in g) per 100 g solution. The advantage of this expression is the ease with which a solution can be prepared, since it simply requires each component to be pre-weighed (for water, a volumetric measurement may be used, e.g. using a measuring cylinder) and then mixed together. Similar terms are parts per thousand (‰), i.e. mg g-1, and parts per million (ppm), i.e.µg g-1.
Per cent concentration (% w]v and % vlv )
For solutes added in solid form, this is the number of grams of solute per 100 mL solution. This is more commonly used than per cent composition, since solutions can be accurately prepared by weighing out the required amount of solute and then making this up to a known volume using a volumetric flask. The equivalent expression for liquid solutes is % v/v.
The principal use of mass/mass or mass/volume terms (including g L-1) is for solutes whose molecular mass is unknown (e.g. polymers), or for mixtures of certain classes of substance (e.g. total salt in sea water). You should never use the per cent term without specifying how the solution was prepared, i.e. by using the qualifier w/w, w/v or v/v, For mass concentrations, it is often simpler to use mass per unit volume, e.g. mgL-1, µg µL-1, etc.
Parts per million concentration (ppm)
This is a non-SI weight per volume (w/v) concentration term commonly used in quantitative analysis such as flame photometry, atomic absorption spectroscopy and gas chromatography, where low concentrations of solutes are to be analysed. The term ppm is equivalent to the expression of concentration as IlgmL-1 (l0-6gmL-1) and a 1.0ppm solution of a substance will have a concentration of 1.0µgmL-1 (1.0 x 1O6gmL-1). A typical procedure for calculations in terms of ppm is shown in Box 6.2.
Parts per billion (ppb) is an extension of this concentration term as ng mL-1 (10-9gmL-1) and is commonly used to express concentrations of very dilute solutions. For example, the allowable concentration of arsenic in water may be 0.05 ppm, but it is more conveniently expressed as 50 ppb.
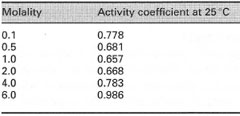
Activity (a) This is a term used to describe the effective concentration of a solute. In dilute solutions, solutes can be considered to behave according to ideal (thermodynamic) principles, i.e. they will have an effective concentration equivalent to the actual concentration. However, in concentrated solutions ( ≥ 0.5 mol L-1), the behaviour of solutes is often non-ideal, and their effective concentration (activity) will be less than the actual concentration [C]. The ratio between the effective concentration and the actual concentration is called the activity coefficient (γ) where,
⇒ Equation 6.3
| γ = | a |
| [C] |
Equation [6.3] can be used for SI units (mol m-3), molarity (mol L-1) or
molality (mol kg-1). In all cases, γ is a dimensionless term, since a and [C] are
expressed in the same units. The activity coefficient of a solute is effectively
unity in dilute solution, decreasing as the solute concentration increases
(Table 6.1). At high concentrations of certain ionic solutes, I' may increase to
become greater than unity. *Note: Activity is often the correct expression for theoretical relationships involving solute concentration (e.g. where a property of the solution is dependent on concentration). However, for most practical purposes, it is possible to use the actual concentration of a solute rather than the activity, since the difference between the two terms can be ignored for dilute solutions. |
|
Equivalent mass (equivalent weight)
Equivalence and normality are outdated terms, although you may come across them in older texts. The magnitude of an equivalent mass (equivalent weight) can be simply identified from the balanced equation for the reaction being considered. Remember that the equivalent mass can change, depending on the reaction, as the following reactions illustrate.
For;
HCI + NaOH → NaCI + H2O
1mol of HCI reacts with 1mol of NaOH, the equivalent mass of HCI is Mr = 36.5 and the equivalent mass of NaOH is also its Mr = 40.
For;
H2S04 + 2NaOH → Na2S04 + 2H2O
since 1mol of H2S04 reacts with 2 mol of NaOH, the equivalent mass of H2S04 is Mr ÷ 2 = 98 ÷ 2 = 49, while the equivalent mass of NaOH is still Mr = 40.
For;
5FeS04 + KMn04 → Fe2(S04)3 + 2MnS04
since 1mol of KMn04 reacts with 5 mol of FeS04, then the equivalent mass of KMn04 is Mr ÷ 5 = 158 ÷ 5 = 31.6, and that of FeS04 is still Mr = 152.
But, for:
H2S04 + Na2CO3 → Na2SO4 + CO2 + H2O
since the reaction is 1:1, the equivalent masses of H2S04 and Na2CO3 are their Mr values, 98 and 106 respectively.
As a result of this possible confusion, the concept of equivalent mass (weight) is rarely used.
Normality A 1 normal solution (1 N) is one that contains one substance per litre of solution. The general formula is:
| normality = | mass of substance per litre |
| equivalent mass |
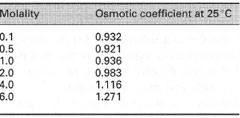
Osmolarity This non-SI expression is used to describe the number of moles of osmotically active solute particles per litre of solution (osmol L-1). The need for such a term arises because some molecules dissociate to give more than one osmotically active particle in aqueous solution. Osmolality This term describes the number of moles of osmotically active solute particles per unit mass of solvent (osmol kg-1). For an ideal solute, the osmolality can be determined by multiplying the molality by n, the number of solute particles produced in solution (e.g. for NaCl, n = 2). |
|
osmolality = molality × n × ø
If necessary, the osmotic coefficients of a particular solute can be obtained from tables (e.g. Table 6.2): non-ideal behaviour means that ø may have values > 1 at high concentrations. Alternatively, the osmolality of a solution can be measured using an osmometer.
Osmotic pressure
This is based on the concept of a membrane permeable to water, but not to solute molecules. For example, if a sucrose solution is placed on one side and pure water on the other, then a passive driving force will be created and water will diffuse across the membrane into the sucrose solution, since the effective water concentration in the sucrose solution will be lower. The tendency for water to diffuse into the sucrose solution could be counteracted by applying a hydrostatic pressure equivalent to the passive driving force. Thus, the osmotic pressure of a solution is the excess hydrostatic pressure required to prevent the net flow of water into a vessel containing the solution. The SI unit of osmotic pressure is the pascal, Pa (= kg m-1 s-2). Older sources may use atmospheres, or bars, and conversion factors are given in Box 9.1. Osmotic pressure and osmolality can be interconverted using the expression 1osmol kg-1 = 2.479MPa at 25°C.
The use of osmotic pressure has been criticized as misleading, since a solution does not exhibit an 'osmotic pressure' unless it is placed on the other side of a selectively permeable membrane from pure water!