pH and buffer solutions

pH is a measure of the amount of hydrogen ions (H⁺) in a solution. It is usual to think of aqueous solutions as containing H⁺ ions (protons), though protons actually exist in their hydrated form, as hydronium ions (H₃O⁺). The proton concentration of an aqueous solution [H⁺] is affected by several factors:

• Ionization (dissociation) of water, which liberates protons and hydroxyl ions in equal quantities, according to the reversible relationship:
  ⇒ Equation [7.1]
  
  H₂O → H⁺ + OH⁻


• Dissociation of acids, according to the equation:
  ⇒ Equation [7.2]
  
  H−A → H⁺ + A-
  
  where H⁻A represents the acid and A-is the corresponding conjugate base. The dissociation of an acid in water will increase the amount of protons, reducing the amount of hydroxyl ions as water molecules are formed (eqn [7.1]). The addition of a base (usually, as its salt) to water will decrease the amount of H⁺, owing to the formation of the conjugate acid (eqn [7.2]).


• Dissociation of alkalis, according to the relationship:
  ⇒ Equation [7.3]
  
  X⁺OH⁻ → X⁺ + OH⁻
  
  where X⁺OH⁻ represents the undissociated alkali. Since the dissociation of water is reversible (eqn [7.1]), in an aqueous solution the production of hydroxyl ions will effectively act to 'mop up' protons, lowering the proton concentration.
  
  Many compounds act as acids, bases or alkalis: those which are almost completely ionized in solution are usually called strong acids or bases, while weak acids or bases are only slightly ionized in solution.
  
  In an aqueous solution, most of the water molecules are not ionized. In fact, the extent of ionization of pure water is constant at any given temperature and is usually expressed in terms of the ion product (or ionization constant) of water, K_w:
  ⇒ Equation [7.4]
  
  K_w = [H⁺] [OH⁻]
  
  where [H⁺] and [OH⁻] represent the molar concentration (strictly, the activity) of protons and hydroxyl ions in solution, expressed as mol L⁻¹. At 25°C,the ion product of pure water is 10⁻¹⁴ mol² L⁻² (i.e. 10⁻⁸ mol⁻² m⁻⁶). This means that the concentration of protons in solution will be 10⁻⁷ mol L⁻¹ (10⁻⁴ mol m⁻³), with an equivalent concentration of hydroxyl ions (eqn [7.1]). Since these values are very low and involve negative powers of 10, it is customary to use the pH scale, where:
  ⇒ Equation [7.5]
  
  pH = −log₁₀[H⁺]
  and [H⁺] is the proton activity.

*Note: While pH is strictly the negative logarithm (to the base 10) of H⁺ activity, in practice H⁺ concentration in mol L^-1 (equivalent to kmol m^-3 in SI terminology) is most often used in place of activity, since the two are virtually the same, given the limited dissociation of H₂0. The pH scale is not SI: nevertheless, it continues to be used widely in chemistry.

The value where an equal amount of H+ and OH− ions are present is termed neutrality: at 25°Cthe pH of pure water at neutrality is 7.0. At this temperature, pH values below 7.0 are acidic while values above 7.0 are alkaline. However, the pH of a neutral solution changes with temperature (Table 7.1), owing to the enhanced dissociation of water with increasing temperature. This must be taken into account when measuring the pH of any solution and when interpreting your results. Always remember that the pH scale is a logarithmic one, not a linear one: a solution with a pH of 3.0 is not twice as acidic as a solution of pH 6.0, but a thousand times as acidic (i.e. contains 1000 times the amount of H+ ions).

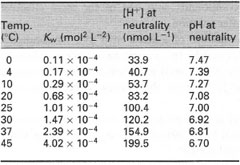Table 7.1 Effects of temperature on the ion product of water (Kw), H+ ion concentration and pH at neutrality.

Therefore, you may need to convert pH values into proton concentrations before you carry out mathematical manipulations (see Box 40.2). For similar reasons, it is important that pH change is expressed in terms of the original and final pH values, rather than simply quoting the difference between the values: a pH change of 0.1 has little meaning unless the initial or final pH is known.